§ 01/92. Mais uma vez, partiremos de um desses problemas aritméticos em que os modernos quase não vêem senão recreação, não sem que os atormente a idéia das virtualidades criadoras que aí descobriria o pensamento tradicional.

§ 02/92. Este se deve ao Sr. Le Lionnais, que nos disseram grande iniciado nesses arcanos e que, assim, teria perturbado a vigília de alguns parisienses. Foi por esse prisma, pelo menos, que ele nos foi proposto por Raymond Queneau, que, grande especialista nos jogos em que não vê o menor objeto em que pôr à prova sua agilidade dialética, e não menos erudito nas publicações reserva¬das em que eles são cultivados, pode ser seguido quando afirma que seu dado é original. Ei-lo.

O problema das doze peças

§ 03/92. Em doze peças de aparência semelhante, uma, que diremos ruim, distingue-se por uma diferença de peso, imperceptível sem um aparelho de medição, diferença esta sobre a qual não se diz se é para mais ou para menos.

§ 04/92. Somos solicitados a encontrar essa peça entre as demais, num total de três pesagens, para as quais dispomos unicamente do ins[91]trumento de uma balança com dois pratos, excluído qualquer peso que sirva de padrão ou qualquer outra tara que não sejam as próprias peças em questão.

§ 05/92. A balança que aqui nos fornecem como aparelho funcionará, para nós, como suporte de uma forma lógica, a que chamamos forma da suspeita ambígua, e a pesagem nos mostrará sua função no pensamento(02). 
_________
02: O estudo aqui desenvolvido situa-se nas análises formais iniciais de uma lógica coletiva, à qual já se referira o texto publicado no número anterior dos Cahiers d'Art, sob o título "O tempo lógico e a asserção de certeza antecipada" (reproduzido nos Escritos, Rio de Janeiro, Jorge Zahar, 1998, p.197-213).
A forma aqui desenvolvida, embora compare a sucessão, não é da ordem do tempo lógico e se situa como anterior em nosso desenvolvimento.
Ela faz parte de nossas abordagens exemplares para a concepção das formas lógicas em que se devem definir as relações do indivíduo com a coleção, antes que se constitua a classe, ou seja, antes que o indivíduo seja especificado.
Essa concepção é desenvolvida numa lógica do sujeito que nosso outro estudo leva a discernir nitidamente, uma vez que, no final dele, chegamos a tentar formular o silogismo subjetivo pelo qual o sujeito da existência assimila-se à essência, para nós radicalmente cultural, a que se aplica o termo humanidade.

Solução do problema

§ 06/92. Esse problema requer uma invenção operatória das mais simples e totalmente à altura do espírito humano. Duvidamos, porém, que esteja ao alcance da mecânica cuja maravilha o nome “máquina de pensar” expressa bem. É que haveria muito a dizer sobre a ordem das dificuldades opostas ao espírito, respectivamente, pelas formas desenvolvidas do jogo dos números e pelas formas mais simples nas quais a questão é saber se contêm implicitamente as outras.

§ 07/92. Assim, para quem quiser experimentar resolver nosso problema, esclareçamos aqui que suas condições devem ser rigorosa¬mente aceitas - isto é, que qualquer resultado constatado, ao se colocarem na balança 2 peças ou 2 grupos de peças (sempre, evidentemente, em número igual), contará como uma pesagem, quer os pratos se equilibrem, quer um deles prevaleça.

§ 09/92. O pequeno número de provas permitidas ordena que se proceda por grupos. A rememoração do dado de que a presença da peça ruim é segura entre as 12 poderia dissuadir-nos de, inicialmente, dividi-las pela metade nos pratos: esse dado, com efeito, por tornar certo que um dos grupos de 6 pesará mais do que o outro, diminui correspondentemente o interesse de tal prova. Mas esse raciocínio se revelará apenas aproximativo.

§ 10/92. A verdadeira justificação do procedimento que tem êxito é que a pesagem numa balança de dois pratos tem três resultados possíveis, conforme eles se equilibrem ou um ou o outro prevaleça. É verdade que, no caso de seu desequilíbrio, nada nos faz reconhecer de que lado está o objeto a que cabe responsabilizar por isso. No entanto, teremos motivos legítimos para operar de acordo com uma distribuição tripartite, forma que encontramos em mais de uma incidência na lógica da coleção.

A primeira pesagem e o problema das quatro

§ 11/92. Retirados de nossas doze peças, portanto, coloquemos na balança dois grupos de quatro.

§ 12/92. A situação do equilíbrio entre eles nos permite encontrar a peça ruim entre as quatro restantes. Problema cuja solução parecerá fácil em duas pesagens, ainda que convenha formulá-la sem precipitação.

§ 13/92. Esclareçamos que, na segunda pesagem, colocaremos em cada prato uma e apenas uma dessas quatro peças. Os pratos ficam em equilíbrio? Nesse caso, as duas peças são boas, e uma delas, oposta numa terceira pesagem a qualquer das restantes, ou evidenciará nesta a peça ruim, ou permitirá situá-la, por eliminação, na última que não foi testada.

§ 14/92. Um dos pratos fica, ao contrário, mais pesado na segunda pesagem? A peça ruim estará entre as duas postas na balança e, sendo portanto certamente boas as duas peças restantes, a situação, semelhante à do caso anterior, será resolvida da mesma ma¬eira, isto é, comparando entre elas uma peça de cada grupo.

§ 15/92. O desenvolvimento do problema mostrará que não é supérfluo assinalar aqui que esse procedimento resolve um problema que pode ser considerado autônomo: o da peça ruim a ser detecta¬da entre quatro, por meio de duas pesagens, isto é, o problema imediatamente inferior ao nosso. As oito peças implicadas em nossa primeira pesagem não intervieram em nada, com efeito, na busca da peça ruim entre as quatro restantes.

O x  da dificuldade e a suspeita dividida

§ 16/92. Voltemos agora a essa primeira pesagem para considerar o caso em que um dos grupos de quatro postos na balança é mais pesado.

§ 17/92. Esse caso é o x do problema. Aparentemente, ele nos deixa a peça ruim a ser detectada entre oito e nos deixa a fazê-lo em duas pesagens, depois de essas duas pesagens se haverem mostrado exatamente suficientes para detectá-la entre quatro.

§ 18/92. Mas, embora a peça ruim continue por ser reconhecida entre oito, a suspeita, digamos, que recai sobre cada uma delas fica desde logo dividida. E aqui tocamos numa dialética essencial das relações do indivíduo com a coleção, na medida em que elas comportam a ambigüidade do a mais ou do a menos.

§ 19/92. Por conseguinte, o resultado da segunda pesagem pode ser formulado como se segue:

§ 20/92. As peças que estão no prato mais carregado só são suspeitas de serem pesadas; as que estão no mais leve só são suspeitas de serem leves demais.

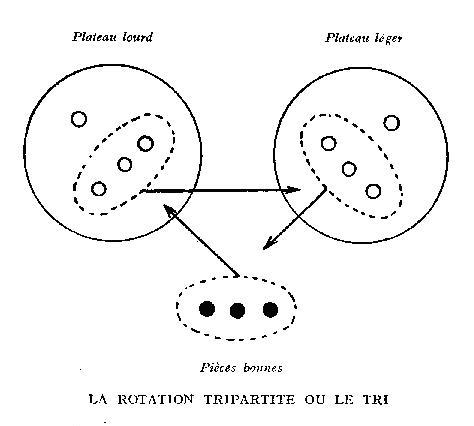
A rotação tripartite ou o tri

§ 21/92. Tal é a raiz da operação que permite resolver nosso problema, e que chamaremos de rotação tripartite, ou então, num trocadilho com seu papel de triagem, o tri.

§ 22/92. Essa operação nos parecerá o nó no desenvolvimento de um drama, quer se trate do problema dos doze, quer, como veremos, de sua aplicação a coleções superiores. Aqui, a terceira pesagem, assim como, nos outros casos, todas as pesagens que se seguirem, se afigurará junto dela tão-somente como um desenlace liquidante.

§ 23/92. Eis o esquema dessa operação:

Figura 01.

§ 24/92. Vemos que se fez intervirem três peças já determinadas como boas, tais como de fato elas nos foram fornecidas, outro resultado da primeira pesagem, nas quatro peças restantes - já que a peça ruim certamente está entre as oito incluídas na pesagem.

§ 25/92. Existe, por outro lado, uma forma da operação que não faz intervirem essas peças - e procede pela redistribuição apenas das peças já na balança, após a exclusão de algumas. Mas, qualquer que seja a elegância dessa economia de elementos, vou ater-me à exposição da forma aqui representada, por diversas razões, a saber:

§ 26/92. 1º) porque a distribuição tripartite dos elementos no teste que precede de imediato a operação fornece necessariamente um número de elementos, depurados da suspeita, sempre mais do que suficiente para que essa forma seja aplicável na extensão ad indefinitum que daremos de nosso problema, e, ainda mais largamente, como veremos, com o complemento essencial que traremos para ele;

§ 27/92. 2º) porque essa forma da operação é mais manejável mental¬mente para os que não se habituaram a concebê-la submetendo-se à prova de seu achado;

§ 28/92. 3º) porque, por último, uma vez resolvida pela pesagem que a conclui, ela é a que deixa menos complexidade para as operações liquidantes.

§ 29/92. Nossa rotação tripartite consiste, pois, no seguinte:

§ 30/92. Em colocarmos três peças boas no lugar de três peças quaisquer do prato mais carregado, por exemplo, e depois usarmos as três peças extraídas desse prato para substituir três peças retiradas do prato mais leve, as quais, a partir daí, ficarão excluídas dos pratos.

A segunda pesagem e a disjunção decisiva

§ 31/92. Basta constatar, numa segunda pesagem, o efeito dessa nova distribuição, para poder concluir, de acordo com cada um dos três casos possíveis, pelos seguintes resultados:

§ 32/92. Primeiro caso: os pratos se equilibram. Todas as peças neles são boas, portanto. A ruim se encontra, nesse caso, entre as três peças excluídas do prato que se mostrou mais leve na primeira pesagem e, como tal, sabemos que ela só pode ser uma peça mais leve do que as outras.

§ 33/92. Segundo caso: mudança de lado do prato que pesa mais. Trata-se, nessa situação, de que a peça ruim mudou de prato. Encontra-se, portanto, entre as três que saíram do prato que se revelara mais pesado na primeira pesagem e, como tal, sabemos que só pode ser uma peça mais pesada do que as outras.

§ 34/92. Terceiro caso: a balança continua inclinada para o mesmo lado que na primeira pesagem. É que a peça ruim se encontra entre as duas que não foram mexidas. E sabemos ainda que, se ela é a peça que permaneceu no prato mais pesado, só pode tratar-se de uma peça mais pesada, e, se for a outra, só pode ser uma peça mais leve que as demais.

A terceira pesagem nos três casos

§ 36/92. Com efeito, uma peça, sobre a qual já se determinou que deve ser mais leve, num dos casos, e mais pesada, no outro, será identificada entre três, numa pesagem que porá na balança duas delas, e na qual ela aparecerá sem ambigüidade; caso contrário, revelará ser a terceira.

§ 37/92. Quanto ao terceiro caso, só temos que juntar as duas peças suspeitas num mesmo prato e guarnecer o outro com duas quaisquer das demais peças, já então depuradas de qualquer suspeita, para que a pesagem aponte a peça ruim. De fato, o prato com as peças suspeitas certamente se manifestará, seja como mais pesado, seja como mais leve que o outro, pois seguramente carrega uma peça pesada demais ou uma peça leve demais, e então saberemos qual delas incriminar, por mais que tenhamos perdido de vista a individualidade de cada uma, ou, dito de outra maneira, de qual prato da segunda pesagem ela proveio.

§ 38/92. Eis então o problema resolvido.

A coleção máxima acessível a n pesagens

§ 40/92. Com efeito, podemos ver que, se duas pesagens são necessárias para identificar a peça ruim numa coleção de quatro, e se três nos permitem resolver o problema das doze, é porque duas pesagens continuam a ser suficientes para descobrir a peça entre oito, desde que uma primeira pesagem tenha repartido duas metades entre as quais se dividem a suspeita do excesso e a da falta. Comprovaremos facilmente que uma aplicação adequada da rotação tripartite permite estender essa regra às coleções superiores, e que quatro pesagens resolvem com facilidade o problema de 36 peças, e assim sucessivamente, multiplicando por 3 o número N de peças todas as vezes que atribuirmos uma unidade a mais ao número n de pesagens permitidas.

§ 41/92. Formulando N como igual a 4 vezes 3n-2, será que determinamos o número máximo de peças acessível à depuração de n pesagens? Bastará tentarmos esse teste para constatar que o número, de fato, é maior, e que a razão disso já está patente no nível de nosso problema.

§ 42/92. O Sr. Le Lionnais, quer por haver obedecido ao preceito tradicional que ordena que, quando alguém sabe dez coisas, só deve ensinar nove, quer por benevolência ou malícia, mostra ter-nos facilitado demais as coisas.

§ 43/92. Apesar de seu dado nos conduzir, de fato, a um procedimento que conserva seu valor, veremos que a compreensão do problema ficaria mutilada para quem não percebesse que três pesagens são capazes de detectar a peça ruim não somente entre doze, mas entre treze.

§ 44/92. Demonstremos isso agora.

O problema das treze

§ 45/92. As oito primeiras peças representam bem tudo o que pode ser posto em jogo na primeira pesagem. E, na eventualidade de todas elas serem boas, caso que contemplamos acima em primeiro lugar, restarão cinco peças, entre as quais duas pesagens nos pare¬cem insuficientes para determinar qual a peça ruim, e elas real¬mente o seriam, se, nesse nível do problema, essas cinco peças fossem os únicos elementos de que dispuséssemos.

§ 46/92. Com efeito, ao examinar o problema limitado a duas pesagens, fica claro que o número de quatro peças é o máximo acessível ao alcance delas. Podemos ainda observar que apenas três peças podem ser efetivamente postas à prova aí, nunca vindo a quarta a ser colocada num dos pratos e só sendo incriminada, no caso extremo, com base no dado que atesta a existência de uma peça ruim.

§ 47/92. A mesma observação é válida para o grupo que estamos considerando como resíduo no problema superior (e valerá apenas para este único caso, porque a detecção de uma peça por eliminação, durante uma pesagem em que ela não entre, como observamos noutros momentos possíveis do problema, decorre do fato de sua presença num grupo ter-se manifestado efetivamente numa pesagem anterior).

§ 48/92. Mas, quando nosso grupo de cinco peças nos é dado como resíduo, o caso não é semelhante ao das quatro peças isoladas. É que, aqui, outras peças, pela pesagem anterior, foram reconhecidas como boas, e uma só já é o bastante para modificar o alcance das duas pesagens que nos são concedidas.

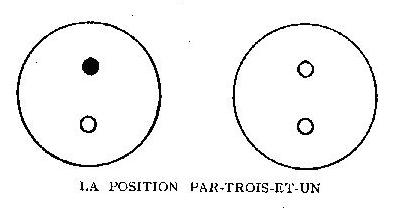
 A posição por-três-e-um

§ 49/92. Com efeito, dignemo-nos considerar a seguinte figura:

Figura 02.

§ 51/92. Dois casos:

§ 52/92. Ou os pratos se equilibrarão e a peça ruim deverá ser encontrada entre as duas restantes das cinco peças, numa pesagem que a revelará numa delas ao testá-la com a mesma peça boa, que aqui ainda nos basta, sem o que teremos de reconhecê-la na última e não testada;

§ 53/92. Ou um dos pratos prevalecerá e constataremos que a suspeita se divide, mas, aqui, de maneira desigual: entre uma única peça, suspeita num sentido, e duas, que o são no sentido inverso.

§ 54/92. Bastará então que tomemos uma das duas restantes, nesse mo¬mento garantidas como boas, para substituí-la pela peça suspeita isolada, e que substituamos por esta última uma das duas suspeitas do par, assim executando a mais reduzida das rotações tripartites, ou rotação tripla, para que o resultado nos seja imediatamente visível numa terceira pesagem:

§ 55/92. - ou o mesmo prato prevalecerá, evidenciando a peça ruim naquela das duas do par que não tiver se mexido;

§ 56/92. - ou haverá equilíbrio, mostrando que a peça ruim é a outra do par que foi expulso do prato;

§ 57/92. - ou, alterando-se o lado que prevalece, a peça ruim será a peça isolada que mudou de prato.

§ 58/92. A disposição decisiva aqui, aquela que ordena a pesagem das três peças suspeitas com uma peça boa, nós a designamos como posiçao por-três-e-um.

§ 59/92. Essa posição por-três-e-um é a forma original da lógica da suspeita. Cometeríamos um erro ao confundi-la com a rotação tripartite, embora ela se resolva nessa operação. Ao contrário, podemos ver que somente essa posição dá à operação sua plena eficácia em nosso problema. E, do mesmo modo que ela aparece como o verdadeiro recurso para resolvê-lo, só ela permite também revelar seu sentido autêntico. É o que demonstraremos agora.

O problema das quarenta

§ 60/92. Passemos, com efeito, ao problema de quatro pesagens, para averiguar até que número de peças se estenderá seu alcance, nas mesmas condições do problema.

§ 61/92. Logo percebemos que uma primeira pesagem pode envolver com sucesso não apenas duas vezes doze peças, conforme a regra sugerida pela primeira resolução do chamado problema das doze, mas também duas vezes treze peças.

§ 62/92. Com efeito, aparecendo o desequilíbrio, a rotação tripartite, efetuada com a contribuição de nove peças boas, é capaz de detectar entre as 26 da primeira pesagem a peça ruim em três pesagens.

§ 63/92. A pesagem depois do tri as separará, com efeito, em dois grupos de nove de suspeita unívoca, em cujo caso uma terceira pesagem de três contra três evidenciará a presença da peça ruim, seja num desses grupos, seja no das três restantes, ou, haja o que houver, ela será enfim isolada por uma quarta e última pesagem, e num grupo de oito, de suspeita dividida, no qual já sabemos encontrar a peça em duas pesagens.

§ 64/92. Mas, havendo-se revelado boas as 26 primeiras peças, restar-nos-ão três pesagens, e é aí que a posição por-três-e-um demonstrará seu valor.

§ 65/92. Para ocupar o campo com um novo tri, ela nos indicará, com efeito, que ponhamos em jogo não apenas quatro peças contra quatro, como sugere o estudo do caso das três pesagens, porém cinco peças contra quatro, complementadas por uma peça boa. Após as demonstrações precedentes, a figura seguinte bastará para demonstrar a solubilidade da posição elas nove peças, quando a ruim for revelada pelo desequilíbrio dos pratos.

§ 66/92. Vemos a seguir o esquema do tri, que, na prova da terceira pesagem, revelará em que grupo de três suspeitas está a peça ruim, bastando uma quarta para isolá-la na totalidade dos casos.

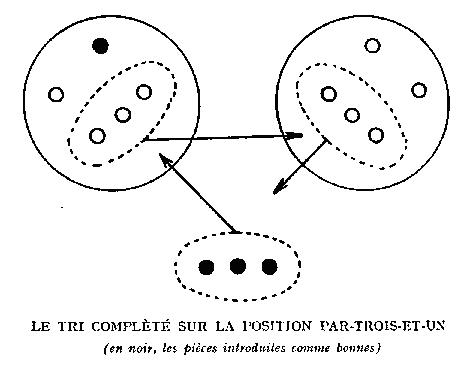
§ 68/92. Daí resultará que, na prova de quatro pesagens:

               26 + 9 + 3 + 1 + 1 = 40 peças são acessíveis.

Figura 03:

A regra geral da condução das operações

§ 69/92. Se reproduzirmos a mesma investigação com um número superior de peças, veremos destacar-se a regra que ordena a condução das operações nessa investigação. Ela é:

§ 70/92. Pôr em jogo o tri, se a peça ruim revelar sua presença entre as envolvidas na primeira pesagem. Caso contrário:

§ 71/92. Introduzir a posição por-três-e-um, desde que disponhamos de uma peça boa, isto é, nas condições aqui expostas, desde a ordenação da segunda pesagem, e renová-la com todas as pesagens que se seguirem, até que a peça ruim revele sua presença numa delas.

§ 72/92. Empregar então a rotação tripartite, que é o momento decisivo de toda a operação. A posição por-três-e-um isola-se num dos grupos, cuja disjunção é efetuada pelo tri.

§ 73/92. Se a pesagem que conclui esse tri identificar a peça no referido grupo, único caso complexo a ser resolvido, repetir nele o tri, com a mesma possibilidade de que se mantenha a posição por-três-e-um e a mesma indicação para resolvê-la, até o esgotamento.

§ 74/92. Algumas regras suplementares deveriam ser acrescentadas para a condução da investigação numa coleção qualquer, isto é, não máxima.

A razão da série das coleções máximas

§ 75/92. Mas estas regras nos permitem ver que cinco pesagens poderão atingir, no máximo:
1 + 1 + 3 + 9 + 27 + 80 = 121 peças;

§ 76/92. - que seis pesagens atingirão:
1 + 1 + 3 + 9 + 27 + 81 + 242 = 364 peças (número singular), e assim sucessivamente:

§ 77/92. - que, sob forma algébrica, a verdadeira fórmula de n anteriormente buscada será tal que:
n = 1 + 1 + 3 + 32 + 33 ... + 3n-1 -1),

§ 78/92. ou: n = 1 + 3 + 32 + 33 ... + 3n-1,
em que vemos que cada número N correspondente a um número n de pesagens é obtido através da multiplicação do número N', que corresponde a (n-1) pesagens, por 3, acrescentando-se uma unidade a esse produto.

§ 79/92. Essa fórmula exprime com perfeita evidência o poder tripartidor da balança a partir da segunda pesagem e, como tal, evidencianos, por seu simples aspecto, que as operações foram ordenadas de tal maneira que preenchem todo o campo numérico oferecido a esse poder.

§ 80/92. Essa confirmação é especialmente importante para os primeiros números da série, por demonstrar a adequação deles à forma lógica da pesagem, e, particularmente, para o número treze, na medida em que o aparente artifício das operações que nos fizeram determiná-lo poderia deixar-nos em dúvida, quer quanto ao fato de uma nova junção permitir superá-lo, quer quanto ao fato de ele deixar vazia uma margem fracionada na dependência de alguma descontinuidade irredutível no arranjo de operações de aspecto dissimétrico.

O sentido do número treze

A forma lógica da suspeita

§ 82/92. Mas, à luz da fórmula de N, podemos avançar mais na compreensão da posição por-três-e-um como forma lógica ao mesmo tempo que demonstrar que, em nosso problema, o dado, embora contingente, não é arbitrário.

§ 83/92. Se o sentido desse problema se relaciona com a lógica da coleção, na qual ele manifesta a forma original que designamos pelo termo suspeita, é porque a norma com que se relaciona a diferença ambígua que ele supõe não é uma norma especificada nem especificadora, mas apenas uma relação de indivíduo para indivíduo dentro da coleção - uma referência não à espécie, mas ao uniforme.

§ 84/92. Isso é o que se evidencia quando, continuando dado que o indivíduo portador da diferença ambígua é único, suprime-se o dado de sua existência na coleção, para substituí-la pelo concurso de um indivíduo padrão, dado fora da coleção.

§ 85/92. Assim, podemos surpreender-nos ao constatar que rigorosamente nada se modificou nas formas nem nos números a serem determinados pelo novo dado aplicado a nosso problema.

§ 86/92. Aqui, certamente, devendo as peças ser testadas até a última, nenhuma poderá ser ti da como ruim na posição de resíduo externo à última pesagem, e o alcance dessa pesagem será diminuído em uma unidade. Mas a peça-padrão, pelo fato de podermos dispor dela no início, nos permitirá introduzir a posição por-três-e-um [103] desde a primeira pesagem e aumentará em uma unidade o grupo incluído nesta. Ora, o dado dessa peça, que parece de tão grande valor para nossa intuição, formada na lógica classificatória, não terá absolutamente nenhum outro efeito.

§ 87/92. Nisso se evidencia que a uniformidade dos objetos do dado em nosso problema não constitui uma classe, e que cada peça tem que ser pesada individualmente.

§ 88/92. De fato, seja qual for o número dos indivíduos em causa em nosso problema, o caso exige ser reduzido ao que é revelado pela pesagem única: à noção absoluta da diferença, raiz da forma da suspeita.

§ 89/92. Essa referência do indivíduo a cada um de todos os demais é a exigência fundamental da lógica da coleção, e nosso exemplo demonstra que ela está longe de ser impensável.

A balança do Juízo Final

§ 90/92. Para exprimi-la no registro de um sonho que obceca os homens, o do Juízo Final, indicaremos que, fixando-se em bilhões o número dos seres que essa grandiosa manifestação implicaria, e só se podendo conceber sua perspectiva a partir da alma como única, a testagem de um por todos os outros, de acordo com a ambigüidade pura da pesagem que representam para nós as figuras tradicionais, se efetuaria, com extrema largueza, em 26 etapas, e portanto a cerimônia não teria nenhuma razão para se arrastar por um tempo prolongado.

§ 91/92. Dedicamos este apólogo àqueles para quem a síntese do particular com o universal tem um sentido político concreto. Quanto aos outros, que se esforcem por aplicar à história de nossa época as formas que demonstramos aqui.

O fenômeno do número  e o retorno à lógica

§ 92/92. Ao procurar novamente nos números uma função geradora para o fenômeno, parecemos retomar a antigas especulações cujo caráter aproximativo fez com que fossem rejeitadas pelo pensamento moderno. É que nos parece, justamente, que é chegado o momento de recuperar esse valor fenomenológico, sob a condição de que sua análise seja levada ao rigor extremo. Provavelmente, aí aparecerão singularidades que, apesar de não deixarem de ter uma analogia estilística com as que se manifestam na física, ou mesmo na pintura ou no novo estilo de xadrez, desconcertarão os espíritos, ali onde sua formação não passa de habito, dando-lhes a sensação de uma quebra da harmonia que chegaria a dissolver os princípios. Se sugerimos precisamente que é preciso efetuar um retorno à lógica, é para reencontrar sua base, sólida como a rocha, e não menos implacável quando entra em movimento.

_________
Nota da BSFREUD:
Esse texto foi escaneado por José Luiz Caon e aqui publicado por sua gentil autorização.
FONTE: LACAN, J.  Outros Escritos: Trad. de Vera Ribeiro. Rio de Janeiro, Jorge Zahar, 2003, pp. 91-105.