Clase 20. del 16 de Mayo de 1962 


Justifico la necesidad de esta elucubración de la superficie, es evidente que lo que les doy es resultado de una reflexión. No han olvidado que la noción de superficie en topología no va de suyo y no está dada como una intuición.

¿Cómo abordar esta noción? A partir de lo que, en lo real la introduce, es decir lo que mostrarla que el espacio no es esta extensión abierta y despreciable como pensaba Bergson. El espacio no es tan vacío como él creía, encierra muchos misterios,

Plantéemos de entrada algunos términos.

Es cierto que una primer cosa esencial en la noción de superficie es la de cara  (face) si habría dos caras o dos lados. Esto va de suyo si, esta superficie, la sumergimos en el espacio. Pero para apropiarnos lo que puede para nosotros tomar la noción  de superficie, es necesario que sepamos lo que nos entrega por sus solas dimensiones. Ver lo que ella puede librarnos en tanto superficie que divide el espacio por sus únicas dimensiones nos sugiere reconstruir el espacio de otro modo que el que creíamos tener por la intuición. En otros términos, les propongo considerar como más evidente (captura imaginaria), más simple, más seguro (ligado a la acción), más estructural partir de la superficie para definir el espacio -del que sostengo estamos muy poco asegurados digamos más bien definir el lugar, que partir del lugar para definir la superficie.

Cf. el lugar en filosofía.

El lugar del Otro tiene ya su lugar en nuestro seminario.

Para definir la cara de una superficie no basta decir que está de un lado y del otro, tanto más cuanto que eso no tiene nada de satisfactorio, y si algo nos da el vértigo pascaliano, es esas dos regiones en las que el plano infinito dividiría todo el espacio.

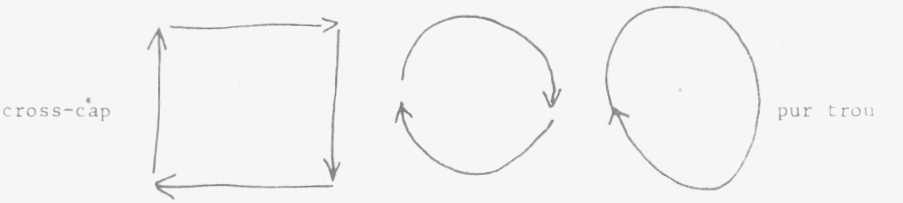
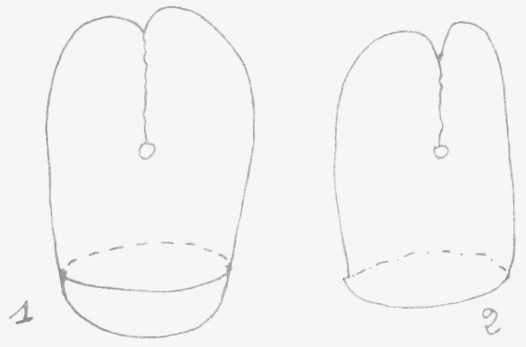
¿Cómo definir esta noción de lado? Es el campo donde puede extenderse una linea, un camino, sin tener que encontrar un borde. Pero hay superficies sin borde: el plano al infinito, la esfera, el toro y muchos otros que se reducen prácticamente a uno solo: el cross-cap o mitra o gorro dibujado al lado (1). El cross-cap en los libros eruditos es esto: cortado para poder insertarse sobre otra superficie (2)

 

Esas tres superficies cerradas elementales a la composición de las cuales todas las otras superficies cerradas pueden reducirse.

Llamaré sin embargo cross-cap a la figura (1). Su verdadero nombre es el plano proyectivo de la teoría de las superficies de Riemann cuyo plano está en la base. Hace intervenir al menos la cuarta dimensión.

Ya la tercera dimensión, para nosotros, psicólogos de la profundidades, hace bastante problema para que la consideremos como poco asegurada. Sin embargo en esta simple figura, el cross-cap,. la cuarta está  implicada necesariamente.

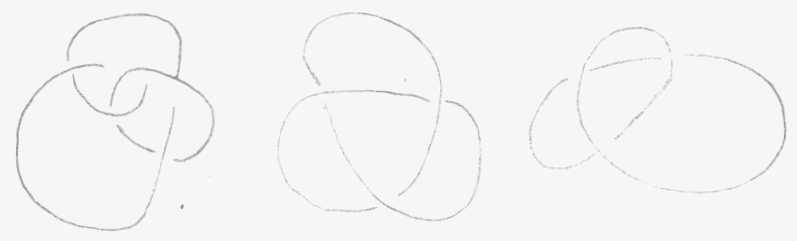
El nudo elemental hecho el otro día con una cuerda, presentifica ya la cuarta dimensión.. No hay teoría topológica válida sin que hagamos intervenir algo que nos lleva a la cuarta dimensión.

 

Si ustedes quieren intentar reproducir ese nudo usando el toro, siguiendo las vueltas y rodeos que pueden hacer en la superficie de un toro, podrían después de muchas vueltas volver sobre una linea que se anilla como el nudo de arriba. No pueden hacerlo sin que la línea se corte a sí misma; como sobre la superficie del toro ustedes no podrán marcar que la línea pasa por encima o por debajo, no hay medio de hacer ese nudo sobre toro. Es por el contrario, perfectamente factible sobre el cross-cap.

Si esta superficie implica la presencia de la cuarta dimensión, es un comienzo de pruebas que el más simple nudo implique la cuarta dimensión. Esta superficie, el cross-cap, voy a decirles como lo pueden imaginar. Esto no impondrá su necesidad por ahí mismo, para nosotros, conducida. Ella no está sin relación con el toro, tiene incluso con el toro la relación más profunda. 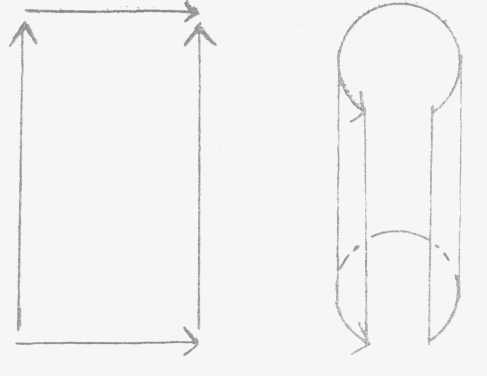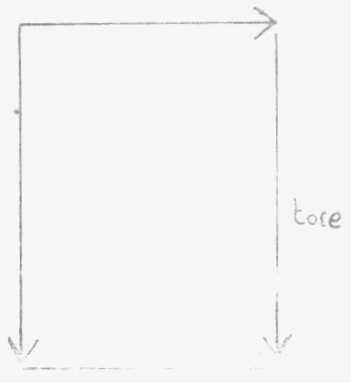El modo más simple de darles esta relación es recordarles como está construido un toro cuando se lo descompone bajo una forma poliédrica, es decir llevándolo a su polígono fundamental. Este polígono fundamental es un cuadrilátero. Si a ese cuadrilátero lo pliegan sobre sí mismo, tendrán un tubo uniendo los bordes.

 

Si se vectorizan esos bordes conviniendo que no puedan ser pegados uno al otro sino los vectores que van en el mismo sentido, aplicándose el comienzo de un vector al punto donde termina el otro vector, -desde entonces se tienen todas las coordenadas para definir la estructura del toro.

Si hacen una superficie cuyo polígono fundamental está así definido por vectores todos en el mismo sentido sobre el cuadrilátero de base, si parten de un polígono así definido, eso haría dos bordes o incluso uno sólo, obtienen lo que les materializo como mitra.

Volveré sobre su función de simbolización de algo y eso será más claro cuando ese nombre sirva de soporte.

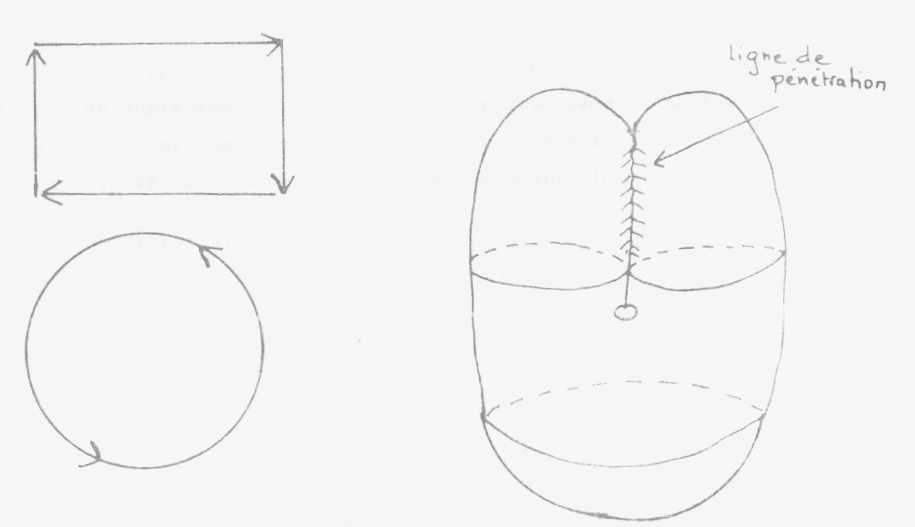
El corte con su pinta de mandíbula, eso no es lo que ustedes creen. Esto es una línea de penetración gracias a la cual lo que está antes...

Por debajo es una semiesfera, arriba la pared de adelante pasa por penetración en el tabique opuesto y vuelve por delante.

¿Porqué ésta forma y no otra? Su polígono fundamental es distinto que el del toro. Un polígono cuyos bordes está marcados por vectores de la misma dirección, y distinto que el del toro, que parte de un punto para ir al punto opuesto, ¿qué se obtiene como superficie?

Desde ahora se desprenden puntos problemáticos de esas superficies. Los he introducido en las superficies sin borde a propósito de la cara. Si no hay borde, ¿cómo definir la cara? Y si nos prohibimos tanto como sea posible sumergir demasiado pronto nuestro modelo en la tercera dimensión, ahí donde no hay borde estaremos asegurados de que hay un interior y un exterior. Es lo que sugiere esta superficie sin borde por excelencia que es la esfera. Quiero alejarlos de esta intuición indecisa: está lo que está dentro y lo que está afuera.

Por tanto para las otras superficies, esta noción de interior y exterior se sustrae. Para el plano infinito no basta, Para el toro, la intuición se sostiene en apariencia suficientemente porque está el interior de una cámara de aire y el exterior. Sin embargo lo que ocurre en el campo por donde este espacio exterior atraviesa el toro, es decir el agujero central, está ahí el nervio topológico de lo que ha constituido el interés del toro, y donde la relación del interior y el exterior se ilustra con algo que puede tocarnos.

Observen que hasta Freud la anatomía tradicional, un tanto sea poco Wissenschaft con Paracelso y Aristóteles, ha siempre tomado cuenta, entre los orificios del cuerpo los órganos de los sentidos como verdaderos orificios.

La teoría psicoanalítica en tanto estructurada por la función de la libido ha hecho una elección bien estrecha entre los orificios y no nos habla de los orificios sensoriales como orificios sino por llevarlos al significante de los orificios de entrada elegidos. Cuando se hace de la escoptofilia una escoptofagia se dice que la identificación escoptofílica es una identiticación oral, como lo hace Fenichel.

El privilegio de los orificios oral, anal y genital, nos retiene en esto, que no son verdaderamente los orificios que dan sobre el interior del cuerpo: el tubo digestivo no es más que una travesía, está abierto sobre el exterior. El verdadero interior es el interior mesodérmico y los orificios que ahí introducen existen bajo la forma de los ojos o las orejas, de la que jamás la teoría psicoanalítica hace mención como tal, excepto sobre la portada de la revista La Psychanalyse. Es el verdadero alcance dado al agujero central del toro; aún cuando no sea un verdadero interior eso nos sugiere algo del orden del pasaje del interior al exterior.

Esto nos da la idea que viene a la inspección de esta superficie cerrada, el cross-cap.

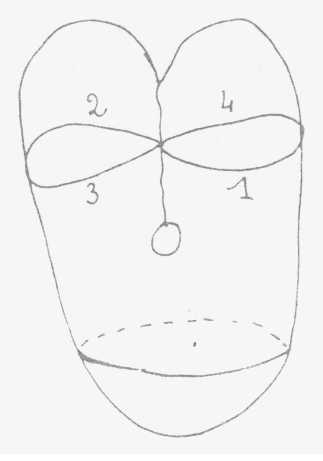
Supongan algo infinitamente plano que se desplace sobre esta superficie pasando del exterior 1 de la superficie cerrada al interior 2 para seguir más lejos en el interior 3 de la línea de penetración donde resurgirá al exterior 4 (de espalda). Esto muestra la dificultad de la definición de la distinción exterior-interior aún cuando se trata de una superficie cerrada, de una superficie sin bordes. No he hecho sino abrir la cuestión para mostrarles que lo importante en esta figura es que esta línea de penetración debe ser considerada por ustedes como nula e inexistente (non avenue). No se la puede materializar en el pizarrón sin hacer intervenir esta línea de penetración, pues la intuición espacial ordinaria exige que se la muestre, pero la especulación no la tiene en cuenta. Se puede hacer deslizar esta línea de penetración indefinidamente. No hay nada del orden de una costura. No hay pasaje posible. A causa de esto el problema del interior y el exterior es planteado en toda su confusión.

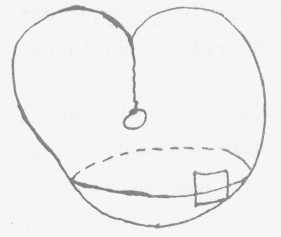
Hay dos órdenes de consideración en cuento a la superficie: métrica y topológica. Hay que renunciar a toda consideración métrica: en efecto a partir de ese cuadrado podría dar toda la superficie. Desde un punto de vista topológico, ésta no tiene ningún sentido. Topológicamente la naturaleza de las relaciones estructurales que constituyen la superficie está presente en cada puntos la cara interna se confunde con la cara exterior para cada uno de sus puntos y de sus propiedades.

Para marcar el interés de esto vamos a evocar una cuestión aún nunca planteada que se refiere al significante: un significante, ¿no tiene siempre por lugar una superficie? Puede parecer una cuestión extraña. Pero tiene al menos el interés, si es planteada, de sugerir una dimensión. En en primer abordaje el gráfico como tal exige una superficie, si es verdad que puede plantearse la objeción de que una piedra levantada, una columna griega, es un significante, y que tiene un volumen, no estén tan seguros de poder introducir la noción de volumen antes de tener bien asegurada la noción de superficie. Sobre todo si, poniendo las cosas a prueba, la noción de volumen no es aprehensible de otra manera que a partir de la envoltura. Ninguna piedra levantada nos ha interesado por otra cosa, no diría que por su envoltura -sería ir a un sofisma- sino por lo que ella envuelve.

Antes de ser volúmenes, la arquitectura se ha hecho de movilizar, componer superficies en torno a un vacío. Las piedras levantadas sirven pera hacer alineamientos o mesas, hacer algo que sirve por el agujero que tienen alrededor.

Pues éste es el resto con el que tenemos que vérnoslas. Si, atrapando la naturaleza de la cara, partí de la superficie con bordes para hacerles notar que el criterio desfallece en las superficies sin borde, si es posible mostrar una superficie sin borde fundamental, donde la definición de la cara no es forzada, en tanto la superficie sin borde no está hecha para permitir resolver el problema del interior y el exterior, debemos tener en cuenta la distinción de una superficie sin con una superficie con: esto tiene la relación más estrecha con lo que nos interesa, a saber el agujero que debemos hacer entrar positivamente como tal en la teoría de las superficies.

No es un artificio verbal. En la teoría combinatoria de la topología general toda superficie triangulable, es decir componible de pequeños trozos triangulares que ustedes pegan unos con otros, toro o cross-cap, puede reducirse por medio de un polígono fundamental a una composición de la esfera a la cual estarían adjuntos más o menos elementos tóricos, elementos de cross-cap y elementos puros agujeros indispensables representados por este vector anillado (bouclé) sobre sí mismo.

Un significante en su esencia más radical no puede ser encarado sino como un corte> < en una superficie, esos dos signos más grande: >, y más pequeño: <, no imponiéndose sino por su estructura de corte inscrita sobre algo donde siempre está marcado, no sólo la continuidad de un plano sobre el cual la serie se inscribirá, sino también la dirección vectorial donde esto se reencontrará siempre? Porqué el significante en su encarnación corporal; es decir vocal, se nos ha presentado siempre como por esencia discontinua? No teníamos pues necesidad de la superficie: la discontinuidad lo constituye. La interrupción en lo sucesivo forma parte de su estructura.

Esta dimensión temporal del funcionamiento de la cadena significante que he articulado de entrada como sucesión, tiene por consecuencia que la escansión introduce un elemento de más que la división de la interrupción modulatorias: introduce la precipitación que ya he insertado en tanto que precipitación en lógica. Es un viejo trabajo: El Tiempo lógico.

El paso que intento hacerles franquear ha comenzado ya a ser trazado, es aquel donde se anuda la discontinuidad con lo que es la esencia del significante, a saber la diferencia. Eso sobre lo cual hemos hecho pivotear, hemos llevado sin pausa esta función del significante, es para atraer vuestra atención sobre esto que, incluso al repetir lo mismo, lo mismo por ser repetido se inscribe como distinto. ¿Dónde está la interpolación de una diferencia? ¿Reside solamente en el corte? -es aquí que la introducción de la dimensión topológica más allá de la escansión temporal nos interesa- ¿o en algo distinto que llamaremos la simple posibilidad de ser diferente, la existencia de una batería diferencial que constituye el significante y por la cual no podemos confundir  sincronía con simultaneidad en la raíz del fenómeno, sincronía que hace que reaparezca lo mismo?

Es como distinto de lo que repite que el significante reaparece, y lo que puede ser considerado como distinguible es la interpolación de la diferencia en la medida en que podemos plantear como fundamento de la función significante la identidad del a y a, a saber que la diferencia reside en el corte, o en la posibilidad sincrónica que constituye la diferencia significante. En todo caso lo que repetimos no es diferente sino por poder ser inscrito.

No queda menos que la función del corte nos importa en primer lugar en lo que puede ser escrito. Y es aquí que la noción de superficie topológica debe ser introducida en nuestro funcionamiento mental por que es sólo ahí que toma su interés la  función del corte.

La inscripción llevándonos a la memoria es una objeción a refutar. La memoria que a nosotros, analistas, nos interesa, debe ser distinguida de una memoria orgánica, aquella que en la misma succión (de lo real) respondería por el mismo modo para el organismo de defenderse que la que mantiene la homeostásis, pues el organismo no reconoce lo mismo que se renueva en tanto diferente. La memoria orgánica  memori-za (meme-orise).

Nuestra memoria es otra cosa: interviene en función del rasgo unario marcando la vez única y tiene por soporte la inscripción. Entre el estimulo y la respuesta, la inscripción, la impresión, debe ser concebida en términos de imprenta gutembergiana. El esbozo de la teoría psicofísica contra la cual nos rebelamos es siempre atomístico; es siempre en la impresión en esquemas de superficie que esta psicofísica toma su primer base. No basta decir que es insuficiente antes de haber encontrado otra cosa.

Pues si es de gran interés ver que la primer teoría de la vida relaciónal  se inscribe en términos interesantes que traducen solamente sin saberlo la estructura misma del significante bajo las formas ocultas de los efectos distintos de contigüidad y continuidad (asociacionismo), es bueno mostrar que lo que estaba reconocido y desconocido como dimensión significante eran los efectos del  significante en la estructura del mundo idealista de la que esta psicofísica no se  ha desprendido jamás.

Inversamente lo que se ha introducido  por la  Gestalt es insuficiente  para dar cuenta de lo que ocurre a nivel de los fenómenos vitales, en razón de una ignorancia fundamental que  se traduce por la rapidez con la cosa tienen por ciertas coordenadas que todo contradice. La pretendida buena forma de la circunferencia que el organismo se obstinarla  sobre todos los planos -subjetivos u objetivos- en buscar reproducir, es contraria a toda observación de las formas orgánicas. Diría a los gestaltistas que una oreja de burro se asemeja a una corneta (cornet), a un aro, a una superficie de Moebius.

Una  superficie de Moebius es la ilustración más simple del cross-cap;  se fabrica con una banda de papel pegando las dos extremidades después de haberla torsionado, de suerte que el ser infinitamente plano que ahí se pasea puede seguirla sin franquear jamás ningún borde. Esto muestra la ambigüedad de la noción de cara. Pues no basta decir que es una superficie uni látera, de una sola cara, como algunos matemáticos formulan. Otra cosa es  la definición formal, no es menos cierto que hay coalescencia para cada  punto de dos caras y es eso lo que nos interesa. Para nosotros que nos contentemos con decirla unilátera bajo pretexto de que esas dos caras están por todos lados presentes, no es menos cierto que podemos manifestar en cada punto el escándalo para nuestra intuición de esa relación de las dos caras.

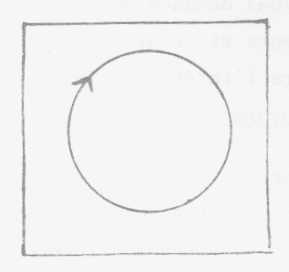
En efecto, en un plano, si trazamos un círculo que gire en el sentido de las agujas del reloj, del otro lado, por transparencia, la misma flecha gira en sentido contrario. El ser infinitamente plano, el pequeño personaje  sobre la superficie de Moebius, si vehiculiza con él un círculo girando en torno de él en el sentido de las agujas del reloj, ese círculo girará siempre en el mismo  sentido, si bien del otro lado de su punto de partida lo que se inscribirá girará en sentido horario, es decir en sentido opuesto a lo que ocurriría en una banda normal, sobre el planos eso no está invertido.

Es por lo que se define a esas superficies como no orientables, y por lo tanto no está menos orientada. El deseo por no ser articulable, no podemos decir sin embargó que no esté articulado. Pues sus pequeñas orejas en la banda de Moebius, por no orientables que sean están más orientadas que en una banda normal. Hagan un cinturón cónico. Denlo vuelta: lo que estaba abierto abajo lo está arriba. Pero den vuelta la banda de Moebius: tendrá siempre la misma forma. Pero cuando ustedes dan vuelta el objeto tendrá siempre la joroba metida en la izquierda, hinchada sobre la derecha;  una superficie no orientable está entonces mucho más orientada que una superficie orientable.

Algo va aún más lejos y sorprende a los matemáticos que reenvían con una sonrisa al lector a la experiencia, y es que, si en esta banda de Moebius con la ayuda de tijeras ustedes trazan un corte a igual distancia de los puntos más accesibles de los bordes (no tiene más que un sólo borde), si ustedes hacen un círculo el corte se cierra, ustedes realizan un circulo, un lazo, una curva cerrada de Jordán. Ahora, este corte, no sólo deja la superficie entera, sino que transforma la superficie no orientable en superficie orientable, es decir en una banda en la que, si colorean uno de los lados, todo un lado quedará blanco, contrariamente a lo que habría ocurrido sobre la superficie de Moebius entera: todo habría sido coloreado sin que el pincel cambie de cara.

La simple intervención del corte ha cambiado la estructura omnipresente de todos los puntos de la superficie. Y si les pido me digan la diferencia entre el objeto anterior al corte y éste, no hay medio de hacerlo, esto para introducir el interés de la función del corte.

El polígono cuadrilátero es originario del toro y del gorro. Si no he introducido nunca la verdadera  verbalización de esta forma  rombo, deseo, uniendo el $ al a en $  a, ese pequeño cuadrilátero debe leerse: el sujeto en tanto marcado por el significante es propiamente, en el fantasma, corte de a .

La próxima vez verán cómo esto nos dará un soporte funcionante para articular la cuestión: cómo lo que podemos definir, aislar a partir de la Demanda como campo del deseo, en su lado inaprehensible, puede por cierta torsión anudarse con lo que, tomado desde otro lado se define como el campo del objeto a, cómo el deseo puede igualarse a a. Es lo que he introducido y lo que les dará un modelo útil hasta en nuestra práctica.