A IDENTIFICAÇÃO - Aula 17 francês

Séminaire du 11 avril 1962

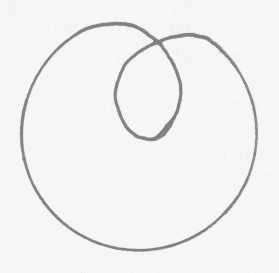
        J'avais avancé que je continuerai aujourd'hui sur le phallus. Eh bien je ne vous en parlerai pas ou bien je ne vous en parlerai que sous cette forme du huit inversé qui n'est pas tellement tranquillisante.

    Ca n'est pas d'un nouveau signifiant qu'il s'agit. Vous allez voir c'est toujours du même dont je parle en somme depuis le début de cette année ; seulement pourquoi je le ramène comme essentiel, c'est pour bien renouveler avec la base topologique dont il s'agit : à savoir ce que ça veut dire l'introduction faite cette année du tore.

    Il n'est pas tellement bien sûr que ce que j'ai dit sur l'angoisse ait été si bien entendu. Quelqu'un de très sympathique et qui lit - parce que c'est quelqu'un d'un milieu où je travaille m'a fort opportunément - je dois dire que je choisis cet exemple parce qu'il est plutôt encourageant - fait remarquer que ce que j'ai dit sur l'angoisse comme désir de l'Autre recouvrait ce qu'on trouve dans Kierkegaard., Dans la première lecture - car c'est tout à fait vrai - vous pensez bien que je m'en souvenais que Kierkegaard pour parler de l'angoisse a évoqué la jeune fille au moment où la première fois elle s'aperçoit qu'on la désire. Seulement si Kierkegaard l'a dit, la différence avec ce que je dis c'est, si je puis dire pour employer un terme kierkegaardien; que je (->p367) (XVII/2) le répète. S'il y a quelqu'un qui a fait remarquer que ce n'est jamais pour rien qu'on le dit "je le dis et je le répète", c'est justement Kierkegaard. Si on éprouve le besoin de souligner qu'on le répète après l'avoir dit, c'est parce que probablement ce n'est pas du tout la même chose de le répéter que de le dire ; et il est absolument certain que, si ce que j'ai dit la dernière fois a un sens, c'est justement en ceci que le cas soulevé par Kierkegaard est quelque chose de tout à fait particulier et comme tel obscurcit, loin d'éclairer, le sens véritable de la formule que l'angoisse est le désir de l'Autre - avec un grand A.

    Il se peut que cet autre s'incarne pour la jeune fille à un moment de son existence en quelque galvaudeux. Cela n'a rien à faire avec la question que j'ai soulevée la dernière fois et avec l'introduction du désir de l'autre comme tel pour dire que c'est l'angoisse, plus exactement que l'angoisse est la sensation de ce désir.

    Aujourd'hui je vais donc revenir à ma voie de cette année et d'autant plus rigoureusement que j'avais dû la dernière fois faire une excursion. Et c'est pourquoi, plus rigoureusement que jamais, nous allons faire de la topologie et il est nécessaire d'en faire parce que vous ne pouvez faire que d'en faire à tout instant, je veux dire, que vous soyez logiciens ou pas, que vous sachiez même le sens du mot topologie ou pas. Vous vous servez par exemple de la conjonction ou . Or, il est assez remarquable mais sûrement vrai que l'usage de cette conjonction n'a été sur le champ de la logique technique, de la logique des logiciens bien articulée, bien précisée, bien mise en évidence qu'à une époque assez récente, beaucoup trop récente pour qu'en somme les effets vous en soient véritablement parvenus ; et c'est pour ça qu'il suffit de lire le moindre texte analytique courant par exemple pour voir qu'à tout instant la pensée achoppe dès qu'il s'agit, non seulement du terme d'identification, mais même de la simple pratique d'identifier quoi que ce soit du champ de notre expérience.

    Il faut repartir des schémas malgré tout, disons-le, inébranlés dans votre pensée, inébranlés pour deux raisons : d'abord parce qu'ils ressortissent à ce que j'appellerai une certaine incapacité à proprement parler propre à la pensée intuitive ou plus simplement à l'intuition, ce qui veut dire aux bases mêmes d'une expérience marquée par l'organisation de ce qu'on appelle le sens visuel. Vous vous apercevrez très facilement de cette impuissance intuitive, si j'ai le bonheur qu'après ce petit entretien vous vous mettiez à vous poser de simples problèmes de représentation sur ce que je vais vous montrer qui peut se passer (->p368) (XVII/3) à la surface d'un tore. Vous verrez la peine que vous aurez à ne pas vous embrouiller. C'est pourtant bien simple un tore : un anneau. Vous vous embrouillerez, et puis je m'embrouille comme vous : il m'a fallu de l'exercice pour m'y retrouver un peu et même m'apercevoir de ce que ça suggérait et de ce que ça permettait de fonder pratiquement.

     L'autre terme est lie à ce qu'on appelle instruction, c'est à savoir que cette sorte d'impuissance intuitive, on fait tout pour 1'encourager, pour l'asseoir, pour lui donner un caractère d'absolu, cela bien sûr dans les meilleurs intentions. C'est ce qui est arrivé par exemple quand en 1741 M. Euler, un très grand nom dans l'histoire des mathématiques, a introduit ses fameux cercles qui, que vous le sachiez ou pas, ont beaucoup fait en somme pour encourager l'enseignement de la logique classique dans un certain sens qui loin de l'ouvrir ne pouvait tendre qu'à rendre fâcheusement évidente l'idée que pouvaient s'en faire les simples écoliers.

    La chose s'est produite parce qu'Euler s'était mis en tête . Dieu sait pourquoi, d'enseigner une princesse, La princesse d'Anhalt Dessau. Pendant toute une période on s'est beaucoup occupé, des princesses, on s'on occupe encore et c'est fâcheux. Vous savez que Descartes avait la sienne : la fameuse Christine. C'est une figure historique d'un autre relief, il en est mort. Ca n'est pas tout à fait subjectif, il y a une espèce de puanteur très particulière qui dégage de tout ce qui entoure l'entité princesse ou prinzessin, nous avons pendant une période d'à peu prés trois siècles, quelque chose qui est dominé par les lettres adressées à des princesses, les mémoires des princesses et ça tient une place certaine dans la culture. C'est une sorte de suppléance de cette tare dont j'ai tenté de vous expliquer la fonction si difficile à comprendre, si difficile à approcher dans la structure de la sublimation courtoise dont je ne suis pas sûr après tout de vous avoir fait apercevoir qu'elle est vraiment la véritable portée. Je n'ai pu vraiment vous en donner que des sortes de projections comme on essaie de figurer dans un autre espace des figures à quatre dimensions qu'on ne peut pas avoir.

    J'ai appris avec plaisir que quelque chose est parvenu à des oreilles qui me sont voisines et qu'on commence à s'intéresser, ailleurs qu'ici, à ce que pourrait être l'amour courtois. C'est déjà un résultat.

    Laissons la princesse et les embarras qu'elle a pu donner à Euler. Il lui a écrit 254 lettres , pas uniquement pour lui faire comprendre les cercles d'Euler. Publiées en 1775 à Londres, elles constituent une (->p369) (XVII/4) sorte de corpus de 1a pensée scientifique à cette date. I1 n'en a surnagé effectivement que ces petits cercles, ces cercles d'Euler qui sont des cercles comme tous les cercles il s'agit simplement de voir l'usage qu'il en a fait. C'était pour expliquer les règles du syllogisme et en fin de compte l'exclusion, l'inclusion et puis ce qu'on peut appeler le recoupement de deux quoi ? de deux champs applicables à quoi ? Mais, mon Dieu applicables à bien des choses, applicables par exemple au champ où une certaine proposition est vraie, applicables au champ où une certaine relation existe, applicables tout simplement au champ où un objet existe.

Vous voyez que l'usage du cercle d'Euler (espace vide - note du claviste) à la multiplicité des logiques telles qu'elles se sont élaborées dans un immense (espace vide-note du claviste) dont la plus grande part tient dans la logique propositionnelle et logique de classe, a été distingué de la façon la plus utile. Je ne peux même pas songer entrer, bien sur dans dans détails que nécessiterait ces élaborations. Ce que je veux

simplement faire ici reconnaître, c'est que vous avez sûrement souvenir de tel ou tel moment de votre existence où vous est parvenue sous cette forme de support une démonstration logique quelconque quelque objet comme objet logique, qu'il s'agisse de proposition, relation classe, voir simplement objet d'existence.

Prenons un exemple au niveau de la logique des classes et représentons cet exemple par un petit cercle à l'intérieur du grand (espace vide-note du claviste) à la classe des vertébrés ; ceci va tout (espace vide-note du claviste) la logique des classes c'est certainement

ce qui au départ (espace vise-note du claviste) de la façon la plus aisée à cette élaboration formelle et qu'on se rapporte à quelque chose de déjà incarné dans une élaboration signifiante, celle de 1a classification zoologique tout simplement qui vraiment en donne le modèle. Seulement l'univers du discours, comme on s'exprime à juste titre, n'est pas un univers zoologique ; et, à vouloir étendre les propriétés de l'univers de la classification zoologique à tout l'univers du discours, on glisse facilement dans un certain nombre de pièges qui vous évitent des fautes (->p370) (XVII/5) et laissent assez vite entendre le signal d'alarme de l'impasse significative.

Un de ces inconvénients est par exemple un usage inconsidéré de la négation. C'est justement à une époque récente que cet usage s'est trouvé ouvert comme possible, à savoir juste à l'époque où on a fait la remarque dans l'usage de la négation ce cercle d'Euler extérieur de l'inclusion devait jouer un rôle essentiel à savoir que ce n'est absolument pas la même chose de parler sans aucune précision par exemple de ce qui est non-homme ou de ce qui est non-homme à l'intérieur des ani maux. En d'autres termes que pour que la négation ait un sens à peu près assuré, utilisable en logique, il faut savoir par rapport à quel en semble quelque chose est nié. En d'au tres termes que pour que la négation ait un sens à peu près assuré, utilisable en logique, il faut savoir par rapport à quel ensemble quelque chose est nié. En d'autres termes si A' est non A, il faut savoir dans quoi il est non A, à savoir ici dans B.

La négation vous la verrez, si vous ouvrez à cette occasion Aristote, entraînée dans toutes sortes de difficultés. Il n'en reste néanmoins pas contestable qu'on n'a nullement ni attendu ces remarques, ni non plus fait le moindre usage de ce support formel - je veux dire qu'il n'est pas normal d'en faire usage pour se servir de la négation - à savoir que le sujet dans son discours fait fréquemment usage de la négation dans des cas où il n'y a pas le moindrement du monde de possibilité de l'assurer sur cette base formelle ; d'où l'utilité des remarques que je vous fais sur la négation en distinguant la négation au niveau de l'énonciation ou comme constitutive de la négation au niveau de l'énoncé. Cela veut dire que les lois de la négation justement au point où elles ne sont pas assurées par cette introduction tout à fait décisive et qui date de la distinction récente de la logique des relations d'avec la logique des classes que c'est en somme pour nous tout à fait ailleurs que là où elle a trouvé son assiette que nous avons à définir le statut de la négation. C'est un rappel, un rappel destiné à vous éclairer rétrospectivement l'importance de ce que depuis le début du discours de cette année je vous suggère concernant l'originalité primordiale par rapport à cette distinction de la fonction de la négation.

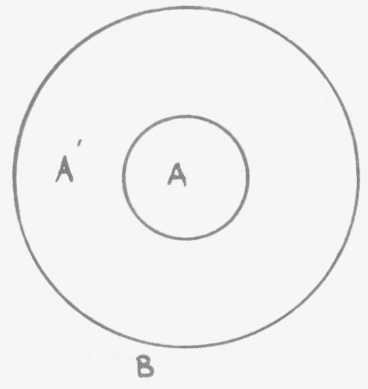
    Vous voyez donc que ces cercles d'Euler, ce n'est pas Euler qui (->p371) (XVII/6) s'en est servi à cette fin ; il a fallu depuis que s'introduise l'oeuvre de Boole, puis de De Morgan pour que ceci soit pleinement articulé.

    Si j'en reviens à ces cercles d'Euler, donc ça n'est pas qu'il en fait lui-même bon usage, mais c'est que c'est avec son matériel, ave l'usage de ces cercles qu'ont pu être faits les progrès qui ont suivi et dont je vous donne à la fois 1'un de ceux qui ne sont pas le moindre ni le moindre notoire, en tout cas particulièrement saisissant, immédiat à faire sentir.

    Entre Euler et de Morgan l'usage de ces cercles a permis une symbolisation qui est aussi utile qu'elle vous paraît du reste implicitement fondamentale, qui repose sur la position de ces cercles qui se structurent ainsi : C'est ce que nous appellerons deux cercles qui se recoupent, qui sont spécialement importants pour leur intuitive qui paraîtra à chacun incontestable si je vous fais remarquer que c'est autour de ces cercles que peuvent s'articuler           deux relations qu'il convient de bien accentuer, qui sont celle d'abord de la réunion : qu'il s'agisse de quoi que ce soit que j'ai énuméré tout à l'heure, leur réunion, c'est le fait qu'après 1'opération de la réunion, ce qui est unifié ce sont deux champs.

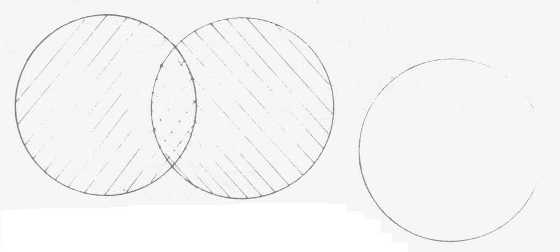
L 'opération dite de la réunion qui se symbolise ainsi ordinairement :

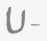c'est précisément ce qui a introduit ce symbole - est, vous le voyez, quelque chose qui n'est pas tout à fait pareil à l'addition, c'est l'avantage de ces cercles que de la faire sentir. Ce n'est pas la même chose que d'additionner par exemple deux cercles séparés ou de les réunir dans cette position.

(->p372) (XVII/7) I1 y a une autre relation qui est illustrée par ces cercles qui se recoupent : c'est celle de l'intersection, symbolisée par ce signe dont la signification est tout à fait différente. Le champ d'intersection est compris dans le champ de réunion.

Dans ce qu'on appelle l'algèbre de Boole, on montre que, jusqu'à un certain point tout au moins, cette opération de la réunion est assez analogue à l'addition pour qu'on puisse la symboliser par le signe de l'addition (+). On montre également que l'intersection est structuralement assez analogue à la multiplication pour qu'on puisse la symboliser par le signe de la multiplication (X).

Je vous assure que je fais là un extrait ultra-rapide destiné à vous mener là où j'ai à vous mener et dont je m'excuse bien sûr auprès de ceux pour qui ces choses se présentent dans toute leur complexité quant aux élisions que tout ceci comporte. Car il faut que nous allions plus loin et sur le point précis que j'ai à introduire, ce qui nous intéresse, c'est quelque chose qui jusqu'à de Morgan - et on ne peut qu'être étonné d'une pareille omission - n'avait pas été à proprement parler mis en évidence comme justement une de ces fonctions qui découlent, qui devraient découler d'un usage tout à fait rigoureux de la logique, c'est précisément ce champ constitué par l'extraction, dans le rapport de ces deux cercles, de la zone d'intersection.

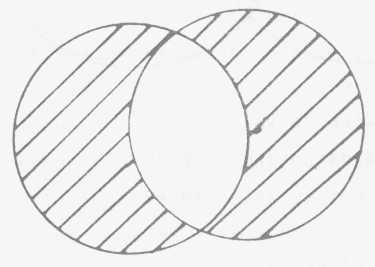
Et considérer ce qui est le produit, quand deux cercles se recoupent, au niveau du champ ainsi défini, c'est-à-dire la réunion moins l'intersection, c'est ce qu'on la différence symétrique.

Cette différence symétrique est ceci qui va nous retenir, qui pour (->p373) (XVII/8) nous -vous verrez pourquoi - est du plus haut intérêt. Le terme différence symétrique est ici une appellation que je vous prie simplement de prendre pour son usage additionnel. C'est comme cela qu'on l'a appelée. N'essayez pas de donner un sens analysable grammaticalement à cette soi disant symétrie. La différence symétrique, c'est ça que cela veut dire, cela veut dire : ces champs, dans les deux cercles d'Euler, en tant qu'ils définissent comme tel un "ou" d'exclusion. Concernant deux champs différents, la différence symétrique marque le champ tel qu'il est construit si vous donnez au "ou", non pas le sens alternatif, mais qui implique la possibilité d'une identité locale entre les deux termes ; et l'usage courant du terme "ou" fait qu'en fait le terme "ou" s'applique ici fort bien au champ de la réunion. Si une chose est A ou B, c'est ainsi que le champ de son extension peut se dessiner, à savoir sous 1a forme première où ces deux champs sont découverts. Si au contraire c'est exclusif A ou B, c'est ainsi que nous pouvons le symboliser, à savoir que le champ d'intersection est exclu.

Ceci doit nous mener à un retour à une réflexion concernant ce que suppose intuitivement l'usage du cercle comme base, comme support de quelque chose qui se formalise en fonction d'une limite. Ceci se définit très suffisamment dans ce fait que sur un plan d'usage courant , ce qui ne veut pas dire un plan naturel, un plan fabricable, un plan qui est tout à fait entré dans notre univers d'outil, à savoir une feuille de papier , nous vivions beaucoup plus en compagnie de feuilles de papier qu'en compagnie de tores. I1 doit y avoir pour ça des raisons mais enfin des raisons qui ne sont pas évidentes. Pourquoi après tout l'homme ne fabriquerait-il plus de tores ? D'ailleurs pendant des siècles, ce que nous avons actuellement sous la forme de feuilles, c'étaient des rouleaux qui devaient être plus familiers avec la notion du volume à d'autres époques qu'à la nôtre. Enfin il y a certainement une raison pour que cette surface plane soit quelque chose qui nous suffise et plus exactement (->p374) (XVII/8) dont nous nous suffisions. Ces raisons doivent être quelque part. Et je l'indiquais tout à l'heure - on ne saurait accorder trop d'importance au fait que, contrairement à tous les efforts des physiciens comme des philosophes pour nous persuader du contraire, le champ visuel quoi qu'on en dise, est essentiellement à deux dimensions : sur une feuille

de papier, sur une surface prati quement simple, un cercle dessiné délimite de la façon la plus claire un intérieur et un extérieur. Voilà tout le secret, tout le mystère, le ressort simple de l'usage qui en est fait dans l'illustration eulérienne de la logique. Je vous pose la question suivante : qu'est-ce qui arrive si Euler, au lieu de dessiner ce cercle, dessine mon huit inversé celui dont aujourd'hui j'ai à vous entretenir ?

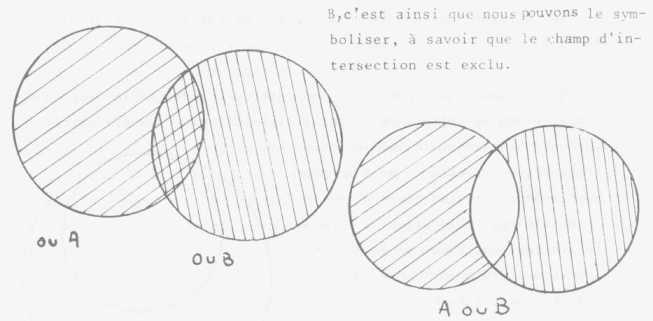
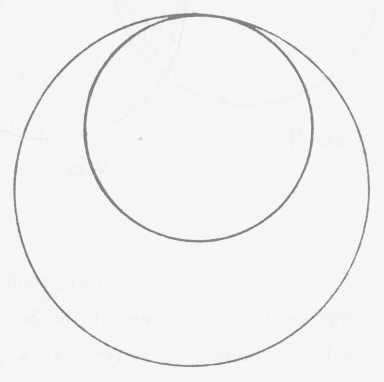
En apparence ce n'est qu'un cas particulier du cercle avec le champ intérieur qu'il définit et la possibilité d'avoir un autre cercle à l'in-

érieur. Simplement le cercle intérieur touche - voilà ce qu'à un premier aspect certains pourront me dire - le cercle intérieur touche à la limite constituée par le cercle extérieur. Seulement c'est quand même pas tout à fait ça, en ce sens qu'il est bien clair, à la façon dont je dessine, que la ligne ici du cercle extérieur continue dans la ligne du cercle intérieur pour se retrouver ici.

Et alors pour simplement tout de suite marquer l'intérêt, la portée de cette très simple forme, je vous suggèrerai que les remarques que j'ai introduites à un certain point de mon séminaire quand j'ai introduit la fonction du signifiant consistaient en ceci : à vous rappeler le paradoxe prétendu tel introduit par la classification des ensembles -rappelez-vous - qui ne se comprennent pas eux-mêmes.

Je vous rappelle la difficulté qu'ils introduisent : doit-on, ces ensembles qui ne se comprennent pas eux-mêmes, les inclure ou non (->p375) (XVII/10) dans l'ensemble des ensembles qui ne se comprennent pas eux-mêmes ? Vous voyez là la difficulté. Si oui, c'est donc qu'ils se comprendront eux-mêmes dans cet ensemble des ensembles qui ne se comprennent pas eux-mêmes. Si non, nous nous trouvons devant une impasse analogue.

    Ceci est facilement résolu à cette simple condition qu'on s'aperçoive à tout le moins de ceci - c'est la solution qu'ont donnée d'ailleurs les formalistes, les logiciens - qu'on ne peut pas parler, disons de la même façon, des ensembles qui se comprennent eux-mêmes et des ensembles qui ne se comprennent pas eux-mêmes. Autrement dit qu'on les exclut comme tels de la définition simple des ensembles, qu'on pose en fin de compte que les ensembles qui se comprennent eux-mêmes ne peuvent être posés comme des ensembles. Je veux dire que loin que cette zone intérieure d'objets aussi considérables dans la construction de la logique moderne que les ensembles, loin qu'une zone intérieure définie par cette image du huit renversé par le recouvrement ou le redoublement dans ce recouvrement d'une classe, d'une relation, d'une proposition quelconque par elle-même, par sa portée à la seconde puissance, loin que ceci laisse dans un cas notoire la classe, la proposition, la relation d'une façon générale, la catégorie à l'intérieur d'elle-même d'une façon en quelque sorte plus pesante plus accentuée, ceci a pour effet de la réduire à l'homogénéité avec ce qui est à l'extérieur.

    Comment ceci est-il concevable ? car enfin on doit tout de même bien dire que, si c'est ainsi que la question se présente, à savoir entre tous les ensembles un ensemble qui se recouvre lui-même, il n'y a aucune raison a priori de ne pas en faire un ensemble comme les autres. Vous définissez comme ensemble par exemple tous les ouvrages concernant ce qui se rapporte aux humanités, c'est à dire aux arts, (->p376) (XVIII/11) aux sciences, à l'ethnographie. Vous en faites une liste ; les ouvrages qui sont des ouvrages faits sur la question de ce qu'on doit classer comme humanités feront partie du même catalogue, c'est-à-dire que ce que je viens même de définir à l'instant to articulant le titre les ouvrages concernant les humanités, fait partie de ce qu'il y a à cataloguer.

    Comment pouvons-nous concevoir que quelque chose qui se pose ainsi comme se redoublant soi-même dans la dignité d'une certaine catégorie puisse se trouver pratiquement nous amener à une antinomies, à une impasse logique telle que nous soyons au contraire contraints de la rejeter ? Voilà quelque chose qui n'est pas d'aussi peu d'importance que vous pourriez le croire puisqu'on a pratiquement vu les meilleurs logiciens y voir une sorte d'échec, de point de butée, de point de vacillation de tout l'édifice formaliste, et non sans raison. Voilà qui pourtant fait à l'intuition une sorte d'objection majeure, toute seule inscrite, sensible, visible dans la forme même de ces deux cercles qui se présentent, dans la perspective eulérienne, comme inclus l'un par rapport à l'autre.

    C'est justement là-dessus que nous allons voir que l'usage de l'intuition de représentation du tore est tout à fait utilisable. Et étant donné que vous sentez bien, j'imagine, ce dont il s'agit, à savoir un certain rapport du signifiant à lui-même, je vous l'ai dit, c'est dans la mesure ou la définition d'un ensemble s'est de plus en plus rapprochée d'une articulation purement signifiante qu'elle a amené à cette impasse, c'est toute la question du fait qu'il s'agit pour nous de mettre au premier plan qu'un signifiant ne saurait se signifier lui-même. En fait c'est une chose excessivement bête et simple ce point très essentiel que le signifiant en tant qu'il peut servir à se signifier lui-même doit se poser comme différent de lui-même. C'est ceci qu'il s'agit de symboliser au premier chef parce que c'est aussi ceci que nous allons retrouver, jusqu'à un certain point d'extension qu'il s'agit de déterminer, dans toute la structure subjective jusqu'au désir y compris.

    Quand un de mes obsessionnels, tout récemment encore après avoir développé tout le raffinement de la science de ses exercices à l'endroit des objets féminins auxquels comme il est commun chez les autres obsessionnels, si je puis dire, il reste attaché par ce qu'on peut appeler une infidélité constante : à la fois impossibilité de quitter aucun de (->p377) (XVII/12) ces objets et extrême difficulté à les maintenir tous ensemble, et qu'il ajoute qu'il est bien évident que dans cette relation, dans ce rapport si compliqué qui nécessite ce si haut raffinement technique, si je puis dire, dans le maintien de relations qui en principe doivent rester extérieures les unes aux autres, imperméables si l'on peut dire les unes aux autres et pourtant liées, que, si tout ceci, me dit-il, n'a pas d'autre fin que de le laisser intact pour une satisfaction dont lui-même ici achoppe, elle doit donc se trouver ailleurs, non pas seulement dans un futur toujours reculé, mais manifestement dans un autre espace puisque de cette intactitude et de sa                   (espace vide -note du claviste) est incapable en fin de compte de dire sur quoi comme satisfaction ceci peut déboucher.

    Nous avons tout de même là sensible, quelque chose qui pour nous pose la question de la structure du désir de la façon la plus quotidienne.

    Revenons à notre tore et inscrivons-y nos cercles d'Euler. Ceci va nécessiter de faire - je m'en excuse - un tout petit retour qui n'est pas, quoi qu'il puisse apparaître à quelqu'un qui entrerait actuellement pour la première fois dans mon séminaire, un retour géométrique - il le sera peut-être tout à fait à la fin mais très incidemment - qui est à proprement parler topologique. Il n'y a aucun besoin que ce tore soit un tore régulier ni un tore sur lequel nous puissions faire des mesures, c'est une surface constituée selon certaines relations fondamentales que je vais être amené à vous rappeler, mais comme je ne veux pas paraître aller trop loin de ce qui est le champ de notre intérêt je vais me limiter aux choses que j'ai déjà amorcées et qui sont très simples.

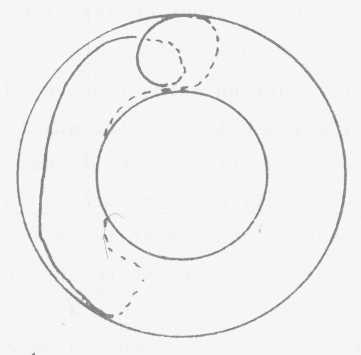
Je vous 1'ai fait remarquer : sur une telle surface, nous pouvons décrire ce type de cercle qui est celui que je vous ai déjà connoté (->p378) (XVII/13) comme réductible, celui qui s'il est représenté par une petite ficelle qui passe à la fin par une boucle, je peux en tirant sur la ficelle le réduire à un point, autrement dit à zéro. Je vous ai fait remarquer qu'il y a deux espèces d'autres cercles ou lacs quelque soit leur étendue car pourrait aussi bien, par exemple celui-là avoir cette forme là . (1)

    Cela veut dire un cercle qui traverse le trou quelle que soit sa forme plus ou moins serrée plus ou moins laxe. C'est ça qui le définit il traverse le trou, il passe de l'espace cité du trou. II est ici représenté en pointillés alors que le 2 est représenté en plein. C'est ceci que cela symbolise : ce cercle n'est pas réductible, ce qui veut dire que si vous le supposez réalisé par une ficelle passant toujours par ce petit arceau qui nous servirait à le serrer nous ne pouvons pas le réduire à quelque chose de ponctiforme, il restera toujours quelle que soit sa circonférence, au centre de la circonférence de ce qu'on peut appeler ici l'épaisseur du tore. Ce cercle irréductible du point de vue qui nous intéressait tout à l'heure, à savoir de la définition d'un intérieur et d'un extérieur, s'il montre d'un côté une résistance particulière, quelque chose qui par rapport aux autres cercles lui confère une dignité éminente, sur cet autre point voici tout à coup qu'il va paraître singulièrement déchu des propriétés du précédent ; car si; ce cercle dont je vous parle, vous le matérialisez par exemple par une coupure avec une paire de ciseaux, qu'est-ce que vous obtiendrez ? Absolument pas, comme dans l'autre cas, un petit morceau qui s'en va et puis le reste du tore. Le tore restera tout entier bien intact sous la forme d'un tuyau ou d'une manche si vous voulez.

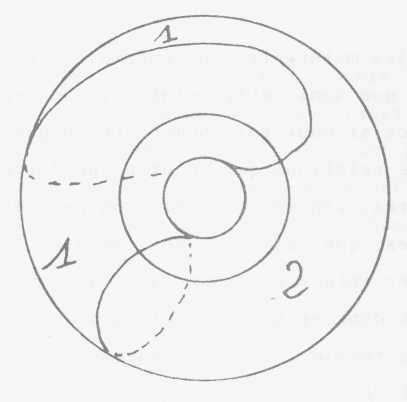
    Si vous prenez d'autre part un autre type le cercle, celui dont je vous ai déjà parlé, celui qui n'est pas celui qui traverse le trou, mais qui en fait le tour, celui-là se trouve dans la. même situation que le précédent quant à l'irréductibilité. I1 se trouve également dans la même situation que le précédent concernant le fait qu'il ne suffit pas à définir un intérieur ni un extérieur. Autrement dit que, si vous 1e suivez, ce cercle, et que vous ouvrez le tore à l'aide d'une paire de ciseaux, vous aurez à 1a fin quoi ? Eh bien, la même chose que dans le cas précédent : ça a la forme du tore, mais c'est une forme qui ne présente une différence qu'intuitive, qui est tout à fait essentiellement (->p379) (XVII/14) la même du point de vue de la structure. Vous avez toujours après cette opération, comme dans le premier cas, une manche, simplement c'est une manche très courte et très large, vous avez une ceinture si vous voulez mais il n'y a pas de différence essentielle entre une ceinture et une manche du point de vue topologique, appelez ça encore une bande si vous voulez.

    Nous voilà donc en présence de deux types de cercles qui de ce point de vue d'ailleurs n'en font qu'un, qui ne définissent pas un intérieur et un extérieur. Je vous fait observer incidemment que, si vous coupez le tore successivement suivant l'un et l'autre, vous n'arrivez pas encore pour autant à faire ce dont il s'agit et que vous obtenez pourtant tout de suite avec l'autre type de cercle 1 (p.12) le premier que je vous ai dessiné, à savoir deux morceaux. 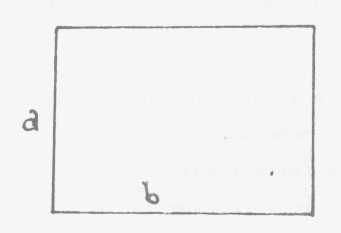Au contraire le tore, non seulement reste bien tout entier, mais c'était, la première fois que je vous en parlais, une mise à plat qui en résulte et qui vous permet de symboliser éventuellement d'une façon particulièrement commode le tore comme un rectangle que vous pouvez en tirant un peu étaler comme une peau épinglée aux quatre points, définir les propriétés de correspondance de ces bords l'un à 1'autre, de correspondance aussi de ses sommets, les quatre sommets se réunissent en un point et avoir ainsi, d'une façon beaucoup plus accessible à vos facultés d'intuition ordinaire, moyen d'étudier ce qui se passe géométriquement sur le tore, c'est-à-dire il y aura un de ces types de cercle qui se représentera par une ligne comme celle-ci,

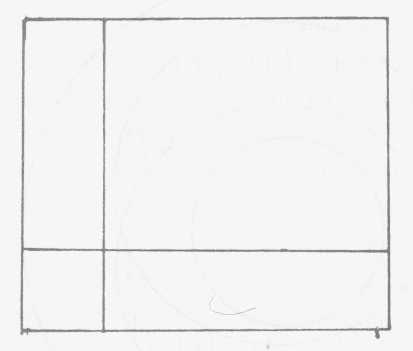
un autre type de cercles par des lignes comme celle-ci représentant deux points posés, définis d'une façon préalable comme étant équivalents sur ce qu'on appelle les bords de la surface étalée mise à plat, si l'on peut dire encore que bien sûr ce ne soit pas d'une véritable mise à plat, la mise à plat comme telle étant impossible puisqu'il ne s'agit (->p380) (XVII/15) pas d'une surface qui soit métriquement identifiable à une surface plane, je le répète purement métriquement, pas topologiquement.

    Où est-ce que ceci nous mène ?

    Le fait que deux sections de cette espèce soient possibles, avec d'ailleurs la nécessité de se regrouper l'une ou 1'autre sans fragmenter d'aucune façon la surface, en la laissant entière, en la laissant d'un seul lambeau, si je puis dire, ceci suffit à définir un certain genre d'une surface. Toutes les surfaces sont loin d'avoir de genre ; si vous faites en particulier une telle section sur une sphère, vous n'aurez toujours que deux morceaux quel que soit le cercle.

    Ceci pour nous conduire à quoi ?

    Ne faisons plus une seule section mais deux sections sur la seule base du tore. Qu'est-ce que nous voyons apparaître ? nous voyons apparaître quelque chose qui assurément va nous étonner tout de suite, c'est à savoir que si les deux cercles se regroupent, le champ dit de la différence symétrique existe bel et bien. Est-ce que nous pouvons dire que pour autant existe le champ de l'intersection ? Je pense que cette figure, telle qu'elle est construite, est suffisamment accessible à votre intuition pour que vous compreniez bien tout de suite et immédiatement qu'il n'en est rien.

(->p381) (XVII/16) C'est à savoir que ce quelque chose qui serait intersection, mais qui ne l'est pas et qui, je dis, pour l'oeil car bien entendu il n'est pas même question un seul instant que cette intersection existe mais qui pour l'oeil est tel que je vous l'ai présenté ainsi sur cette figure telle qu'elle est dessinée, se trouverait peut-être quelque part ici (voir schéma) de ce champ parfaitement continué d'un seul bloc, d'un seul lambeau avec ce champ là qui pourrait analogiquement, de la façon la plus grossière pour une intuition justement habituée à se fonder aux choses qui se passent uniquement sur le plan, correspondre à ce champ externe où nous pourrions définir, par rapport à deux cercles d'Euler se recoupant, le champ de leur négation, à savoir si ici nous avons le cercle A et ici le cercle B, ici nous avons A' négation de A et nous avons ici B' négation de B, et il y a quelque chose à formuler concernant leur intersection à ces champs extérieurs éventuels.

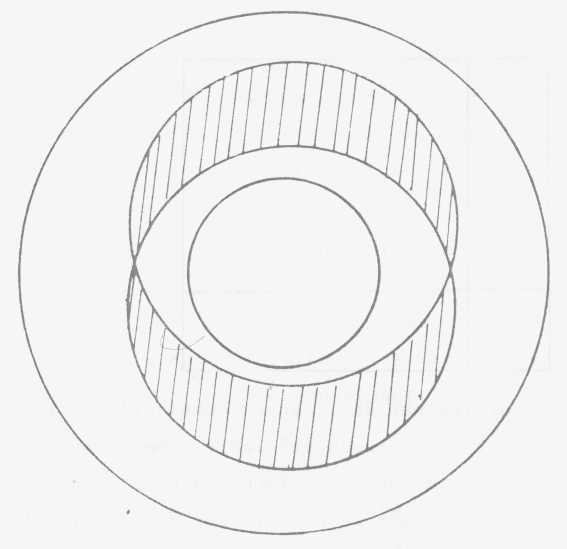
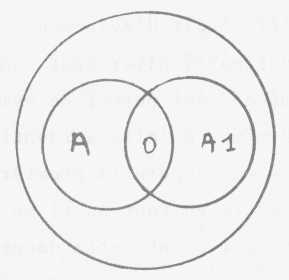
Ici nous voyons donc illustré de la façon la plus simple par la structure du tore ceci que quelque chose est possible, quelque chose qui peut s'articuler ainsi : deux champs se recoupant, pouvant comme tels définir leur différence en tant que différence symétrique, mais qui n'en sont pas moins deux champs dont on peut dire qu'ils ne peuvent se réunir et qu'ils ne peuvent pas non plus se recouvrir, en d'autres termes qu'ils ne peuvent ni servir à une fonction de "ou..., ou...", de réunion, ni servir à une fonction de multiplication (intersection) par soi même. Ils ne peuvent littéralement pas se reprendre à la deuxième puissance, ils ne peuvent pas réfléchir 1'un par l'autre et l'un dans l'autre ; ils n'ont pas d'intersection ; leur intersection est exclusion d'eux-mêmes. Le champ où l'on attendrait l'intersection est le champ où l'on sort de ce qui les concerne, où on est dans le non-champ. Ceci est d'autant plus intéressant qu'à la représentation de ces deux cercles nous pouvons substituer notre huit inversé de tout à l'heure.

(->p382) (XVII/17)

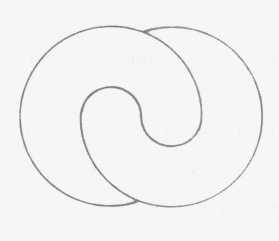
Nous nous trouvons alors devant une forme qui pour nous est encore plus suggestive. Car essayons de nous rappeler ce à quoi j'ai pensé tout de suite à les comparer, ces cercles qui font le tour du trou du tore : là quelque chose, vous ai-je dit, qui a rapport avec l'objet métonymique, avec l'objet du désir en tant que tel. Qu'est-ce que ce huit inversé, ce cercle qui se reprend lui-même à l'intérieur de lui-même, qu'est-ce que c'est, si ce n'est un cercle qui à la limite se redouble et se ressaisit, qui permet de symboliser - puisqu'il s'agit d'évidence intuitive et que les cercles eulériens nous paraissent particulièrement convenables à une certaine symbolisation de la limite - qui permet de symboliser cette limite en tant qu'elle se reprend elle-même, qu'elle s'identifie à elle-même. Réduisez de plus en plus la distance qui sépare la première boucle, disons de la seconde et vous avez le cercle en tant qu'il se saisit lui-même. Est-ce qu'il y a pour nous des objets qui aient cette nature, à savoir, qu'ils subsistent uniquement dans cette saisie de leur autodifférence ? Car de deux choses l'une : ou ils la saisissent, ou ils ne la saisissent pas.. 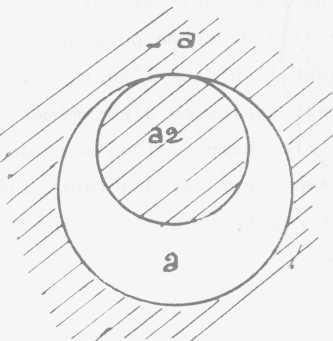Mais il y a une chose en tout cas que tout ce qui se passe à ce niveau de la saisie implique et nécessite, c'est que ce quelque chose exclut toute réflexion de cet objet sur soi-même. Je veux dire que supposez que ce soit petit a dont il s'agisse, comme je vous l'ai déjà indiqué que c'était ce à quoi ces cercles allaient nous servir, ceci veut dire que a 2, le champ ainsi défini, est le même champ que ce qui est là, c'est-à-dire non -a ou -a.

a2 = -a
Supposez pour l'instant, je n'ai pas dit que c'était démontré, je vous dis que je vous fournis aujourd'hui un modèle, un support intuitif à quelque chose qui est précisément ce dont nous avons besoin concernant la constitution du désir. Peut-être vous paraîtra-t-il plus accessible, plus immédiatement à votre portée d'en faire le symbole de l'autodifférence du désir à lui-même et le fait que c'est précisément à son redoublement sur lui-même que nous voyons (->p383) (XVII/18) apparaître ce qu'il enserre, se dérobe et fuit vers ce qui l'entoure. Vous direz : arrêtez-vous, suspendez-vous ici, car ce n'est pas réellement le désir que j'entends symboliser par la double boucle de ce huit intérieur mais quelque chose qui convient beaucoup mieux à la conjonction du petit a, de l'objet du désir comme tel avec lui-même. Pour que le désir soit effectivement, intelligemment supporté dans cette référence intuitive à la surface du tore, il convient d'y faire entrer comme de bien entendu la dimension de la demande. Cette dimension de la demande, je vous ai dit d'autre part que les cercles enserrant 1'épaisseur du tore comme telle pouvaient servir très intelligiblement à la représenter et que quelque chose d'ailleurs qui est en partie contingent, je veux dire lié à une aperception toute extérieure, visuelle, elle même trop marquée de l'intuition commune pour n'être pas réfutable, vous le verrez, mais enfin telle que vous êtes forcés de vous représenter le tore, à savoir quelque chose comme cet anneau, vous voyez facilement combien aisément ce qui se passe dans la succession de ces cercles capables de suivre en quelque sorte en hélice et selon une répétition qui est celle du fil autour de la bobine, combien aisément 1a demande dans sa répétition, son identité et sa distinction nécessaires, son déroulement et son retour sur elle-même, est quelque chose qui trouve facilement à se supporter de la structure du tore.

Ce n'est pas là ce que j'entends aujourd'hui répéter une fois de plus. D'ailleurs, si je ne faisais que le répéter ici, ce serait tout à fait insuffisant ; c'est au contraire quelque chose sur lequel je voudrais attirer votre attention, à savoir ce cercle privilégié qui est constitué par ceci que c'est non seulement un cercle qui fait le tour du trou central, mais que c'est aussi un cercle qui le traverse. En d'autres termes qu'il est constitué par une propriété topologique qui confond, qui additionne la boucle constituée autour de l'épaisseur du tore avec celle qui se ferait d'un tour fait par exemple autour du trou intérieur.

Cette sorte de boucle est pour nous d'un intérêt tout à fait privilégié ; car c'est elle qui nous permettra de supporter, d'imager les relations comme structurales de la demande et du désir.

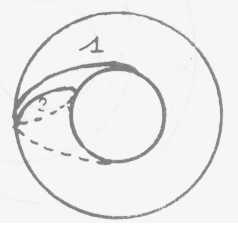
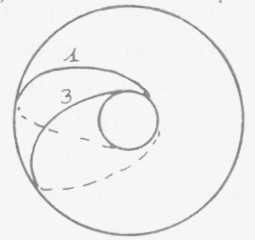
(->p384) (XVII/19) Voyons en effet ce qui se peut se produire concernant de telles boucles observez qu'il peut y en avoir d'ainsi constituées, qu'une autre qui lui est voisine s'achève, revienne sur elle-même, sans du tout couper la première. Vous le voyez étant donné ce que j'ai là essayé de bien articuler, de bien dessiner à savoir la façon dont ça se passé de l'autre côté de cet objet que nous supposons massif parce que c'est comme ça que vous l'intui-

tionnez si facilement et qui évidemment ne l'est pas, la ligne du cercle 1 passe ici, l'autre ligne 3 passe un peu plus loin. Il n'y a aucune espèce d'intersection de ces deux cercles.

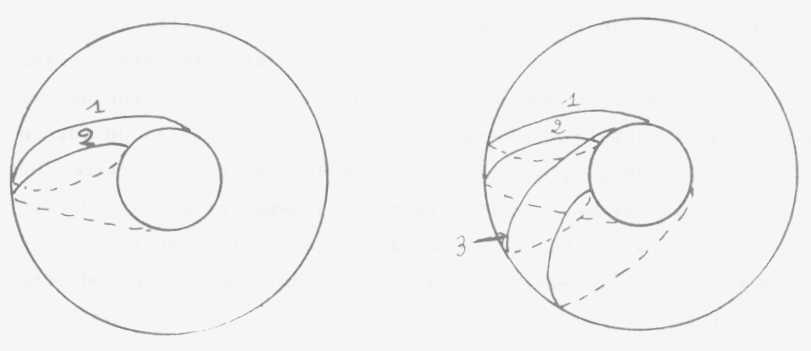
Voici deux demandes qui tout en impliquant le cercle central avec ce qu'il symbolise- à l'occasion, l'objet, et dans quelle mesure il est effectivement intégré à la demande, c'est ce que nos développements ultérieurs nous permettent d'articuler - ces deux demandes ne comportent aucune espèce de recoupement, aucune espèce d'intersection et même aucune espèce de différence articulable entre elles encore qu'elles aient le même objet inclus dans leur périmètre. Au contraire il y a un autre temps de circuit, celui qui passe effectivement du l'autre côté du tore, mais loin de se rejoindre à lui-même au point d'où il est parti amorce ici une autre courbe pour venir une seconde fois passer ici et revenir à son point de départ.

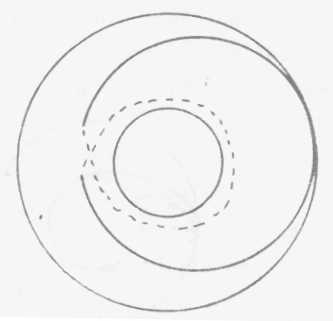
(->p385) (XVII/20) Je pense que vous avez saisi ce dont il s'agit : il s'agit de rien moins que de quelque chose d'absolument équivalent à la fameuse courbe du huit inverse dont je vous ai parlé tout-à-1'heure. Ici les deux boucles représentent la réitération, la réduplication de la demande et comportent alors ce champ de différence à soi-même, d'autodifférence qui est celui sur lequel nous avons mis l'accent tout à l'heure, c'est-à-dire qu'ici nous trouvons le moyen de symboliser d'une façon sensible, au niveau de la demande elle-même, une condition pour qu'elle suggère, dans toute son ambiguïté et d'une façon strictement analogue à la façon dont elle est suggérée dans la réduplication de tout à l'heure de l'objet du désir lui-même, la dimension centrale constituée par le vide du désir. Tout ceci je ne vous l'apporte que comme une sorte de proposition d'exercices, d'exercices mentaux d'exercices avec lesquels vous avez à vous familiariser, si vous voulez pouvoir dans le tore trouver pour la suite la valeur métaphorique que je lui donnerai quand j'aurai dans chaque cas, qu'il s'agisse de l'obsessionnel, de l'hystérique, du pervers, voire même du schizophrène, à articuler le rapport du désir et de la demande. C'est pourquoi c'est sous d'autres formes, sous 1a forme du tore déployé, mis à plat de tout à l'heure que je vais essayer de bien vous marquer à quoi correspondent les divers cas que j'ai jusqu'ici évoqués, à savoir les deux premiers cercles par exemple qui étaient deus cercles qui faisaient le trou central et qui se recoupaient en constituant à proprement parler la même figure de différence symétrique qui est celle des cercles d'Euler.

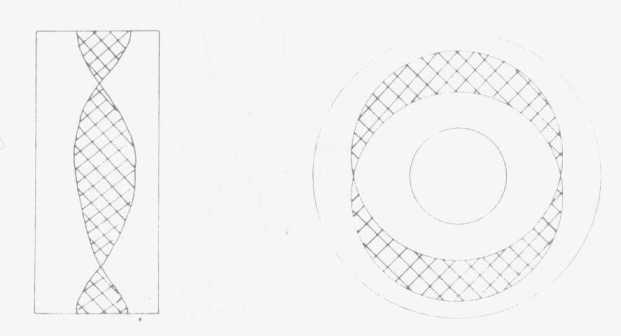
(->p386) (XVII/21) Voici ce que ça donne sur le tore étalé, certainement de cette façon figure plus satisfaisante que ce que vous voyiez tout à 1'heure en ceci que vous pouvez toucher du doigt ce fait qu'il n'y a pas symétrie, disons entre les quatre champs, deux par deux, tels qu'ils sont définis par le recoupement des deux cercles.

Vous auriez pu tout à l'heure vous dire, et certainement pas d'une façon qui aurait été le signe de peu d'attention, qu'à dessiner les choses ainsi et à donner une valeur privilégiée à ce que j'appelle ici différence

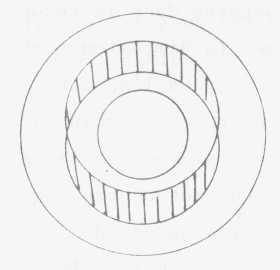
symétrique je ne fais là que quelque chose d'assez arbitraire puisque les deux autres champs dont je vous ai fait remarquer qu'ils se confondent occupaient peut-être par rapport à ces deux-ci une place symétrique. Vous voyez qu'il n'en est rien, à savoir que les champs définis par ces deux, secteurs, de quelque façon que vous les raccordiez -et vous pourriez le faire - ne sont d'aucune façon identifiables au premier champ.

L'autre figure, à savoir celle du huit inversé se présente ainsi :

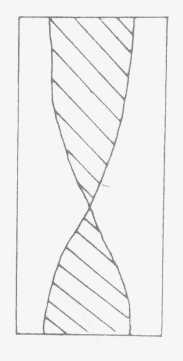
La non symétrie de ces deux champs est encore plus évidente : les deux cercles que j'ai dessinés ensuite successivement sur le pourtour du tore comme définissant deux cercles de la demande en tant qu'ils ne se recoupent pas, les voici ainsi symbolisés. Il y en a un que nous (->p387) (XVII/22) pouvons identifier purement - je parle des deux cercles de la demande tels que je viens de les définir en tant qu'ils incluaient en plus le trou central - l'un peut très facilement se définir, se situer sur le tore étalé comme une oblique reliant en diagonale un sommet au même point qu'il est réellement au bord opposé ; au sommet opposé de sa

position AB. La seconde boucle que AA j'avais dessinée tout à l'heure se symboliserait ainsi : commençant en un point ici quelconque, nous avons ici A' ici E', un point C qui est le même que ce point C' et finissant en B' : A' B' CB' .

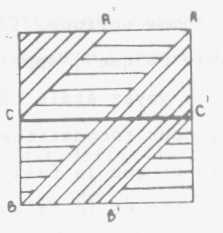
Il n'y a ici aucune possibilité de distinguer le champ qui est en

.I1 n'a aucun privilège par rapport à ce champ-ci. Il n'en est pas de même si au contraire le huit intérieur que nous symbolisons, car alors il se présente ainsi :

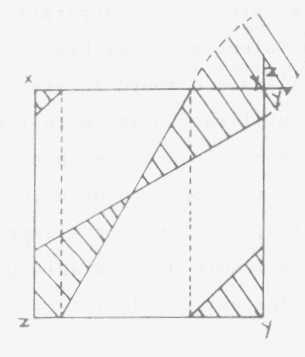
    Voici l'un de ces champs : il est défini par les parties ombrées ici. I1 n'est manifestement pas symétrique avec ce qui reste de l'autre champ, de quelque façon que vous vous efforciez de le recomposer. I1 est bien évident que vous pouvez le recomposer de la façon suivante, que cet élément-là - mettons le x - venant ici, cet y venant là et ce z venant ici vous aurez la forme définie par l'autodifférence dessinée par le huit intérieur.

    Ceci dont nous verrons 1'utilisation par 1a suite peut vous paraître quelque peu fastidieux, voir superflu au moment même où j'essaie pour vous de l'articuler. Néanmoins je voudrais vous faire remarquer à quoi ça sert. Vous le voyez bien : tout l'accent que je porte sur la définition de ces champs est destiné à vous marquer en quoi ils sont utílisables, ces champs de 1a différence symétrique et de ce que j'appelle (->p388) (XVII/23) 1'autodifférence, en quoi ils sont utilisables pour une certaine fin et en quoi ils se soutiennent comme existant par rapport à un autre champ qu'ils excluent.

    En d'autres termes à établir leur fonction dissymétrique, si je me donne tellement de peine, c'est qu'il y a une raison : la raison est celle-ci : c'est que le tore, tel qu'il est structuré purement et simplement comme surface, il est très difficile de symboliser d'une façon valable ce que j'appellerai sa dissymétrie. En d'autres termes, quand vous le voyez étalé à savoir sous la forme de ce rectangle dont il s'agira, pour reconstituer le tore, que vous conceviez primo que je le replie et que je fais un tube, secondo que je ramène un bout du tube sur l'autre et je fais un tube fermé, il n'en reste pas moins que ce que j'ai fait dans un sens j'aurais pu le faire dans l'autre.

    Puisqu'il s'agit de topologie, et non de propriétés métriques, la question de la plus grande longueur d'un côté par rapport à l'autre n'a aucune signification. Que ce n'est pas ceci qui nous intéresse, puisque c'est la fonction réciproque de ces cercles qu'il s'agit d'utiliser. Or justement dans cette réciprocité ils apparaissent pouvoir avoir des fonctions strictement équivalentes. Aussi bien cette possibilité est elle à la base de ce que j'avais d'abord laissé pointer apparaître dès le début pour vous dans l'utilisation de cette fonction du tore comme d'une possibilité d'image sensible à son propos, c'est que chez certains sujets, certains névrosés par exemple, nous voyons en quelque sorte d'une façon sensible la projection, si l'on peut s'exprimer ainsi, des cercles même du désir dans toute la mesure où il s'agit pour eux, si je puis dire, d'en sortir dans des demandes exigées de l'Autre. Et c'est ce que j'ai symbolisé en vous montrant ceci : c'est que, si vous dessinez un tore, vous pouvez simplement en imaginer un autre qui enserre, si l'on peut dire, de cette façon le premier ; il faut bien voir que chacun des cercles qui sont des cercles autour du trou peuvent avoir par simple roulement leur correspondance dans des cercles qui passent à travers le trou de l'autre tore, qu'un tore en quelque sorte est toujours transformable en tous ses points en un tore opposé.

Ce qu'il s'agit donc de voir c'est ce qui originalise une des fonctions circulaires, celle des cercles pleins par exemple par rapport à ce que nous avons appelé à un autre moment les cercles vides. Cette différence existe très évidemment, on pourrait par exemple la symboliser, la (->p389) (XVII/24) formaliser en indiquant par un petit signe sur la surface du tore étalé en rectangle si vous le voulez l'antériorité selon laquelle se ferait le repliement, et si nous appelons ce côté petit a et ce coté petit b, noter par exemple petit a inférieur à petit b, ou inversement. Ce serait là une notation à laquelle jamais personne n'a songé en topologie et qui aurait quelque chose de tout à fait artificiel, car on ne voit pas pourquoi un tore serait d'aucune façon un objet qui aurait une dimension temporelle.

A partir de ce moment, il est tout à fait difficile de 1e symboliser autrement, encore qu'on voit bien qu'il y a là quelque chose d'irréductible et qui fait même à proprement parler toute la vertu exemplaire de l'objet torique.

Il y aurait une autre façon d'essayer de l'aborder. I1 est bien clair que c'est pour autant que nous ne considérons le tore que comme surface et ne prenant ses coordonnées que de sa propre structure que nous somme mis devant cette impasse, grosse pour nous de conséquences puisque si évidemment les cercles dont vous voyez que je vais tendre à les faire servir pour y

fixer la demande bien entendu dans ses rapports avec d'autres cercles qui ont rapport avec le désir, s'ils sont strictement réversibles, est-ce que c'est là quelque chose que nous désirons avoir pour notre modèle ? Assurément pas. C'est au contraire du privilège essentiel du trou central qu'il s'agit ; et par conséquent le statut topologique que nous cherchons comme utilisable dans notre modèle, va se trouver nous fuir et nous échapper. C'est justement parce qu'il nous fuit et nous échappe qu'il va se révéler fécond pour nous.

    Essayons une autre méthode pour marquer ce dont les mathématiciens, les topologistes se passent parfaitement dans la définition, l'usage qu'ils font de cette structure du tore en topologie : eux-mêmes, dans la théorie générale des surfaces, ont mis en valeur la fonction du tore comme élément irréductible de toute réduction des surfaces à ce qu'on appelle une forme normale. Quand je dis que c'est un élément irréductible, je veux dire qu'on ne peut réduire le tore à autre chose. On peut imaginer des formes de surface aussi complexes que vous voudrez mais il faudra toujours tenir compte de la fonction tore dans toute planification, si je puis m'exprimer ainsi, dans toute triangulation dans la théorie des surfaces. Le tore ne (->p390) (XVII/25) suffit pas, il y faut d'autres termes, il y faut nommément la sphère, il y faut ce à quoi je n'ai même pas pu même aujourd'hui encore faire allusion, introduire la possibilité de ce qu'on appelle cross-cap et la possibilités de trous.

    Quand vous avez la sphère, le tore, le cross-cap et le trou, vous pouvez représenter n'importe quelle surface qu'on appelle compacte, autrement dit une surface qui soit décomposable en lambeaux. 1l y a d'autres surfaces qui ne sont pas décomposables, mais nous les laissons de côté.

    Venons-en à notre tore et à la possibilité de son orientation. Est-ce que nous allons pouvoir la faire par rapport à la sphère idéale sur laquelle il s'accroche ? Nous pouvons, cette sphère, toujours l'introduire, à savoir qu'avec une suffisante puissance de souffle n'importe quel tore peut venir à se représenter comme une simple poignée à la surface d'une sphère qui est une partie de lui-même suffisamment gonflée. Est-ce que par l'intermédiaire de la sphère nous allons pouvoir, si je puis dire, replonger le tore dans ce que - vous le sentez bien - nous cherchons pour l'instant, à savoir ce troisième terme qui nous permette d'introduire la dissymétrie dont nous avons besoin entre les deux types de cercles ?

    Cette dissymétrie pourtant si évidente, si intuitivement sensible, si irréductible même et qui est pourtant telle qu'elle se manifeste à propos comme étant ce quelque chose que nous observons toujours dans tout développement mathématique : la nécessité pour que ça démarre, d'oublier quelque chose au départ, ceci vous 1e retrouvez dans toute espèce de progrès formel, ce quelque chose d'oublié et qui littéralement se dérobe à nous, nous fuit dans le formalisme, est-ce que nous allons pouvoir le saisir, par exemple dans la référence de quelque close qui s'appelle tuyau à la sphère ?

    En effet, regardez bien ce qui se passe et ce qu'on nous dit que toute surface formalisable peut nous donner dans la réduction la forme normale? On nous dit ceci se ramènera toujours à une sphère, avec quoi ? avec des tores insérés sur celle-ci et que nous pouvons valablement symboliser ainsi. Je vous passe la théorie, l'expérience prouve que c'est strictement exact. Qu'en outre nous aurons ce qu'on appelle des cross-cap. ( ces cross-cap, je renonce à vous en parler aujourd'hui, il faudra que je vous en parle parce qu'ils nous rendront le plus grand service. Contentons-nous de considérer le tore.

    (->p391) (XVII/26) I1 pourrait nous venir à l'idée qu'une poignée comme celle-ci, qui ne serait non pas extérieur à la sphère, mais intérieure avec un trou pour y entrer,

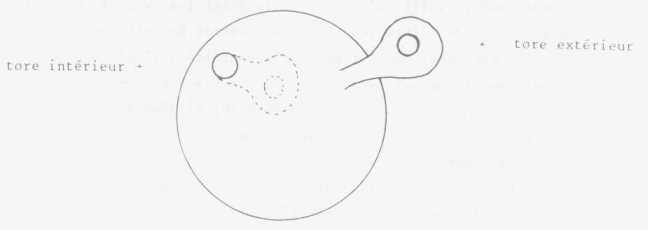
c'est quelque chose d'irréductible, d'inéliminable et qu'il faudrait en quelque sorte distinguer les tores extérieurs et les tores intérieurs.

En quoi est-ce que ceci nous intéresse ? Très précisément à propos d'une forme mentale qui est nécessaire à toute notre intuition de notre objet. En effet, dans la perspective platonicienne, aristotélicienne, eulérienne d'un Umwelt et d'un Innenwelt, d'une dominance mise d'emblée sur la division de l'intérieur et l'extérieur, est-ce que nous ne placerons pas tout ce que nous expérimentons, et nommément en analyse, dans la dimension de ce que j'ai appelé l'autre jour le sous-terrain, à savoir le couloir qui s'en va dans la profondeur, autrement dit, au maximum, je veux dire dans sa forme la plus développée selon cette forme.

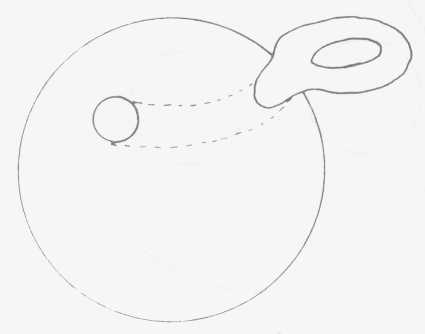
Il est extrêmement exemplaire de faire sentir à ce propos la non-indépendance absolue de cette forme ; car je vous le répète pour autant qu'on arrive à des formes réduites qui sont les formes inscrites, vaguement croquées au tableau dans le dessin pour donner un support à ce je dis , il est absolument impossible de soutenir même un instant, dans la différence l'originalité éventuelle de la poignée intérieure (->p392) (XVII/27) par rapport à la poignée extérieure, pour employer les termes techniques. I1 vous suffit, je pense, d'avoir un peu d'imagination pour voir que s'il s'agit de quelque chose que nous matérialisons en caoutchouc il suffit d'introduire le doigt ici (voir schéma) et d'accrocher de l'intérieur l'anneau central de cette poignée telle qu'elle est ainsi constituée pour l'extraire à l'extérieur selon exactement une forme qui sera celle-ci, c'est-à-dire une tore exactement le même, sans aucune espèce de déchirure, ni même à proprement parler d'inversion. Il n'y a aucune inversion : ce qui était intérieur, à savoir le cheminement ainsi de l'intérieur du couloir, devient extérieur parce que ça l'a toujours été. Si cela vous surprend, je peux encore l'illustrer d'une façon plus simple qui est exactement la même parce qu' il n'y a aucune différence entre ceci et ce que je vais vous montrer maintenant et que je vous avais montré dès le premier jour, espérant vous faire sentir de quoi il s'agissait. Supposez que ce soit au milieu de son parcours, ce qui est exactement la même chose du point de vue topologique que le tore soit pris dans la sphère ; vous avez ici un petit couloir qui chemine d'un trou à un autre trou. Là je pense qu'il vous est suffisamment sensible qu'il n'est pas difficile, simplement en faisant bomber un peu ce que vous pouvez saisir par le couloir avec le doigt, de faire apparaître une figure qui sera à peu près celle ci : de quelque chose qui est ici une poignée et dont les deux trous communiquant avec l'intérieur sont ici en pointillés.

Nous arrivons donc à un échec de plus, je veux dire à 1'impossibilité, par une référence à une troisième dimension ici représentée par la sphère, de symboliser ce quelque chose qui mette le tore, si l'on peut dire, dans son assiette, par rapport à sa propre dissymétrie. Ce que nous voyons une fois de plus se manifester, c'est ce quelque chose qui est introduit par ce très simple signifiant que je vous ai apporté (->p392) (->XVII/28) d'abord du huit intérieur, à savoir la possibilité d'un champ intérieur comme étant toujours homogène au champ extérieur.

Ceci est une catégorie tellement essentielle à marquer, à imprimer dans votre esprit que j'ai cru devoir aujourd'hui, au risque de vous lasser, voir de vous fatiguer, insister pendant une seule de nos leçons. Vous en verrez, je l'espère, l'utilisation dans la suite.